Lesson 2 – Engineering Method#
Learning Outcomes#
Understand the first four steps of the engineering method.
Understand and employ a systematic approach to solving problems.
Given a single measure of merit, choose the best available option.
Given options with multiple measures of merit, evaluate and choose the best option.
Use engineering notation to communicate large and small numbers in a convenient, abbreviated format.
Clearly articulate the answer to an engineering question.
The Engineering Method#
The Engineering Method is a set of seven steps that can be used to effectively build something to accomplish a particular task. The steps start with adequately defining the project and continue through actual construction and evaluation of the design. The seven steps in the Engineering Method are:
Define the Problem – This includes explicitly stating assumptions, requirements, and measures of merit. Do not just repeat the wording of the problem. Think about your approach, obstacles you expect to encounter, and assumptions you will need to make.
Collect Data – We can’t make reasonable decisions without data, and oftentimes, we will need to collect data that seems, at the moment, irrelevant. At the same time, we must make an effort to pare down the data as we learn more about the problem so that we are not overwhelmed by the data.
Create Viable Solutions – Once we have collected the data, we may examine all possible solutions in order to determine which solutions do and do not meet the requirements. Sometimes, we may have been given all possible solutions by contractors, and other times, we will have to brainstorm all possible solutions. A solution that meets all requirements is said to be a viable solution. Because engineering analysis requires us to model scientific phenomenon, we must support our determination of viable solutions with all of the math and assumptions used in making the determination. Engineers expect their math to be checked for correctness; therefore, the math should be clearly explained. Tables, diagrams, and spreadsheets are often useful to explain the process. If any component or option is deemed inviable, the rationale for that decision must be clearly explained.
Analyze Solutions and Select the Best Solution – Various decision-making tools may be used to select the best solution from a set of viable solutions, but in ECE 315, we will focus on using decision matrices to select the best solution. Decision matrices will be explained in more detail later in this reading, but for now, know that decision matrices are used to analyze viable solutions and select the best option among them based off of a subjective weighing scheme.
Construct Solution – This step refers to actually building the selected solution. This is beyond the scope of this course, but it is important to implement the selected solution.
Test and Evaluate – After the system is constructed, we need to ensure it does what it is supposed to do. In the Air Force, there are entire Wings dedicated to this step (i.e. AFOTEC at Kirtland AFB and 46th Test Wing at Eglin AFB), and many people spend their entire careers in this capacity. It is critical to document the results of any tests and evaluations.
Reflection – Document your conclusions and lessons learned. What would you do differently? What sort of solution would you like to see? Do we need to go back and change, fix, or upgrade anything? How do you know that the chosen solution is the right solution for this problem?
The design projects in this class will require you to use steps 1-4 and 7 of the engineering method. In ECE 315, you will be part of a team whose goal is to complete multiple design projects. If you split tasks to expedite the process, it is highly recommended that you check your teammates’ work. If your teammates do not produce quality work (calculations, reasoning, presentations) and you don’t correct them, your grade will be impacted.
Systematic Approach to Problem Solving#
In addition to using the Engineering Method to build something useful, we want to emphasize a systematic approach to solving problems. This systematic method is very similar to the Engineering Method but gives us a more practical framework for solving the kinds of small- scale problems we encounter in this course. You will see this same approach employed for the example problems in the readings throughout this course. The systematic approach contains four steps: Understand, Identify, Plan and Solve. These steps are explained in more detail below.
Understand - First of all, we must understand what is happening in the scenario we are presented with. Here, we assemble a mental (and perhaps physical) picture of the situation and what all the pieces are doing. By explaining the scenario in our own words, we are better able to understand what we know and what we don’t know. For example, if the problem relates to a power transmission line, we might ask:
a. Who is consuming the power?
b. Where else is power consumed in the scenario?
c. Is there loss in the transmission line?
d. What is the transformer doing for us?
Once we have this complete mental picture, we can move on to the next step.
Identify - in this step, we identify the key parts of the problem. We focus on the following categories:
a. Knowns - information given in the problem description. By making an organized list of information we have available, we will better see where we should go.
b. Unknowns – what we are being asked to find. It is equally as important to identify exactly what we are trying to solve. Sometimes, knowing exactly what we are being asked to find is more difficult than finding the answer.
c. Assumptions – bits of information that are not given but are required to solve the problem. If you think back to your Physics class, you may remember assuming that every pulley is frictionless. Obviously, this is not the case in real life, but it is important to write down your assumptions so that others can follow your work. It will also help when looking for partial credit in this class.
Taking the time to go write all this down may seem menial, but it is important to get in the habit of explicitly identifying the information we have so we can know when we have reached a solution. Additionally, as we construct our plan, identifying the key parts of the problem will give us a concise list of information that will help us reach a solution.
Plan - Now that we understand what is going on and have identified all the relevant information, we can make a step-by-step plan to find our unknowns. Many times, you will be looking for more than one unknown quantity. Since those quantities may be dependent on one another, be sure to factor in the order of operations.
During this step, you may formulate the plan in one of two ways: either by starting from the end goal and working backwards or by starting with something you know and deducing what the next step might be. Either way works, but you will likely find one works better than the other for you, so pick that method and stick with it. Be sure to write out exactly what you intend to do in each step and the equation(s) you will use during that step.
Solve - The final step is to combine the information you identified in step 2 with the plan you formulated in step 3. Many call this “plug and chug”, which means you plug the known information into the equations you identified in the planning step. The result of this step is a final answer, clearly indicated with a box or circle.
Decision Matrices#
Oftentimes, you find yourself trying to make a decision based on two or more different criteria or parameters. For example, suppose you want to use your cadet loan to buy a new car. You’re having difficulties making a choice, but you know that you want to make a decision based solely on cost and fuel economy. In order to decide which car is the best for you, you must either convert both parameters to a common metric (e.g., cost or fuel economy) or find a way to combine the two measures into a single score. The danger of converting to a common metric is that, while the measures may seem the same, their importance may vary. For example, depending on the situation you are in, the one-time cost of buying a car may be more important to you than the recurring cost of fuel economy, and vice versa. Common metrics don’t allow us to compare the importance of the various metrics, and for that reason, we will not be using common metrics in ECE 315. In this class, we will be combining the two metrics into a single score, and we will do that with decision matrices.
Decision matrices are tables that allow us to systematically work through the metrics of each options to arrive at a single quantified score for each option. Once we’ve identified each option’s final score, it will be a simple matter to select the option with the best score. This is done by following a 5-step process:
Step 1: Identify the Measures of Merit
The first thing you need to do is list the metrics we want to use in our decision. These metrics are called measures of merit since each one should have some sort of quantifiable value for each option under consideration. In our car-buying example, the cost of the car will be in units of dollars ($), and the value will be somewhere in the thousands of dollars. On the other hand, the fuel economy will be in units of miles per gallon, and the value will be somewhere in the tens of miles per gallon. These values for each option will be need to be listed in the decision matrix.
Step 2: Normalization
Once you have identified all measures of merit and listed their values in the decision matrix, the next step will be convert these values into a unit-less range of scores. This process is known as normalization. If we think of the different measure of merit values as raw values, then normalization works to convert all the raw values to normalized scores that do not have units and fall somewhere between 0 and 1. To begin normalization, we must determine whether to maximize or minimize each measure of merit. Going back to our car buying example, we would prefer a smaller cost, so we would minimize that measure of merit. On the other hand, we would prefer a larger fuel economy, so we want to maximize that measure of merit. From this, we will be able to see that the “best raw value” for cost will be the smallest cost among all of the cars you are considering, and the “best raw value” for fuel economy will be the largest fuel economy. Then, we can use the following equations to find the normalized scores. In the following equations, the “raw value” refers to the value of the measure of merit being normalized for each of the options being considered.
Minimize: \({Score}_{norm} = \ \ \frac{Best\ Raw\ Value}{Raw\ Value}\) Maximize:\({\ Score}_{norm} = \ \ \frac{Raw\ Value}{Best\ Raw\ Value}\)
As you can see from the minimizing equation, we will have a smaller value (the best raw value) divided by a larger value (the raw value), so that should make the normalized score less than 1. With the maximizing equation, we will always have a smaller value (the raw value) divided by a larger value (the best raw value), resulting in a normalized score less than 1. To create a normalized score for the option that has the best raw value, we plug the best raw value in for the raw value in these equations, leading to a normalized score of 1 in both cases.
Key Concept: When normalizing, the score should always be less than or equal to one. If you end up with a normalized score greater than one, then you used the wrong equation.
Step 3: Weighting
Once you have normalized all your measures of merit, you still need to combine them into a single score. This combination step gives us the opportunity to increase the value of one measure over the other by assigning weights to the measures of merit. In our car-buying example, if you would prefer to pay more now in order to save in future gasoline costs, you should give fuel economy a higher weight than cost. You could give cost a weight of 40%, or 0.4, and fuel economy a weight of 60%, or 0.6. Therefore, we assign weights to each measure of merit based on their relative importance where the weights must total to 100%, or 1.0. In our example, we could have picked any weights for cost and fuel economy as long as they summed to 100%.
Key Concept: When assigning weights to measures of merits, the weights must sum to 100%.
Note: Assigning weights can be a subjective process, and for this reason, you need to clearly state the weights you chose and fully justify why you chose those weights. This is all a part of sound engineering analysis!
Once we have assigned the weights, we calculate the weighted score for each measure of merit for each option. We do this by multiplying the normalized score by the measure of merit’s weight.
\[Score_{weighted} = Score_{norm} \times Weight\]The weights for each measure of merit and the weighted scores for each option’s measures of merit can now be entered into the decision matrix.
Step 4: Calculate Each Option’s Final Score
Now that you have all the weighted scores for each option, you’ll need to sum up the weighted scores for each option to determine the option’s total score as follows:
At the end of this step, we should have a final score for each option that falls somewhere between 1 and 0 which will go in the last column of the decision matrix.
Step 5: Select the Best Option
The final step is to compare each options final score to pick out the best option. In this class, the option with the highest score final score will be the best option.
Let’s now look at some examples for how we can use a decision matrix to pick the best option for a given situation.
Example Problem 1: A team has identified two options for the power supply of a UAS. After finding the efficiencies of the two options, you research the costs for each option. Since Option B requires a larger transformer and more efficient converter, it costs more. If Option A costs $600 and Option B costs $1500, which should the government buy? Assume the two measures of merit are cost and efficiency and are equally important.
Understand: We need to compare options with multiple measures of merit to select a winner. This requires us to use step 4 of the Engineering Method.
Identify:#
Knowns: Measures of merit for the options we are comparing are summarized in the following table:
Cost |
Efficiency |
|
|---|---|---|
Option A |
$600 |
95.13% |
Option B |
$1500 |
99.19% |
Unknowns:#
What is the best solution?
Normalized Cost and Efficiency scores for both systems
Weighted Cost and Efficiency scores for both systems
Total Cost and Efficiency scores for both systems
Assumptions: Since the measures are equally important, each will have a weight of 50%, or 0.5.
Plan: In order to determine which power supply the Government should buy, we must determine the normalized and weighted for the measures of merit for each option then use the weighted scores to calculate the total score for each option. The following expansion of the decision matrix is helpful in doing so.
Cost |
Efficiency |
Total |
|||||
|---|---|---|---|---|---|---|---|
Weight |
0.5 |
0.5 |
|||||
Value |
Norm Score |
Weight Score |
Value |
Norm Score |
Weight Score |
||
Option A |
$600 |
95.13% |
|||||
Option B |
$1500 |
99.19% |
To populate this table, we should calculate the normalized score for each option first, then the weighted score for each option, then the total scores.
Normalization:#
Minimize: \({Score}_{norm} = \ \ \frac{Best\ Raw\ Value}{Raw\ Value}\)
Maximize:\({\ Score}_{norm} = \ \ \frac{Raw\ Value}{Best\ Raw\ Value}\)
Weighting:#
\[{Score}_{weighted} = {Score}_{norm}*Weight\]
Total Score:#
\[Score_{total} = Score_{weighted_{cost}} + Score_{weighted_{efficiency}}\]
Best Choice: the option with the highest total score
Solve: Use the plan we created above
Normalization:#
a. Cost: We recognize that cost should be minimized; therefore, the best cost is option A, which receives a normalized cost score of 1.0.
\[{Score}_{Norm_{A,cost}} = \frac{Best\ Raw\ Value_{cost}}{Raw\ Value_{A,cost}} = \ \frac{600}{600} = 1.0\]To calculate Option B’s cost score, we use the same equation, except we use Option B’s cost for the raw value:
\[{Score}_{Norm_{B,cost}} = \frac{Best\ Raw\ Value_{cost}}{Raw\ Value_{B,cost}} = \ \frac{600}{1500} = 0.4\]One way to view this number is that in terms of cost, Option B is only 40% as good as Option A.
b. Efficiency: Since we want to maximize efficiency, the best efficiency is Option B, so it receives a normalized score of 1.0. What about Option A’s efficiency score? If we use the wrong equation for efficiency (the one for minimizing a measure), we have:
\[{Score}_{Norm_{A,efficiency}} = \frac{Best\ Raw\ Value_{efficiency}}{Raw\ Value_{A,efficiency}} = \ \frac{99.19\%}{95.13\%} = 1.043\]Clearly, something is wrong since the answer is above 1. We need to be maximizing efficiency, but we used the equation to minimize it. Looking at the values given to us, Option B has the better efficiency, but we just gave a higher score to Option A. We should use the correct equation for maximizing a measure:
\[{Score}_{Norm_{A,efficiency}} = \frac{Raw\ Value_{A,efficiency}}{Best\ Raw\ Value_{efficiency}} = \ \frac{95.13\%}{99.19\%} = 0.959\]This time, the value is less than 1. This result makes more sense.
Weighting: To get the weighted score, we multiply the normalized score by the weighting. In our assumptions, we noted that each has a weighting of 0.5. Therefore, we have:
c. Cost:
\[{Score}_{weighted_{A,cost}} = {Score}_{Norm_{A,cost}}*Weight_{cost} = 1.0*0.5 = 0.5\]\[{Score}_{weighted_{B,cost}} = {Score}_{Norm_{B,cost}}*Weight_{cost} = 0.4*0.5 = 0.2\]
d. Efficiency:
\[{Score}_{weighted_{A,efficiency}} = {Score}_{Norm_{A,efficiency}}*Weight_{efficiency} = 0.959*0.5 = 0.480\]
\[{Score}_{weighted_{B,efficiency}} = {Score}_{Norm_{B,efficiency}}*Weight_{efficiency} = 1.0*0.5 = 0.5\]
Total Score: this is simply the sum of the weighted scores:
Now, we can populate our decision matrix:
Cost |
Efficiency |
Total |
|||||
|---|---|---|---|---|---|---|---|
Weight |
0.5 |
0.5 |
|||||
Value |
Norm Score |
Weight Score |
Value |
Norm Score |
Weight Score |
||
Option A |
$600 |
1 |
0.500 |
95.13% |
0.959 |
0.480 |
0.980 |
Option B |
$1500 |
0.4 |
0.200 |
99.19% |
1.000 |
0.500 |
0.700 |
Best choice: Option A has the highest score and is the best choice.
Answer: The Government should buy Option A.
Example Problem 2: Let’s do the same analysis but this time, we’ll account for a difference in importance by assigning a weight of 70% to efficiency (since it’s a long-term recurring cost) and only 30% to the cost.
Understand: We need to compare two different options using different weights.
Identify:
Knowns: We have the cost and efficiency information from the previous problem, but we can also reuse the normalized scores since the raw values did not change. Therefore, we have the following decision matrix.
Cost |
Efficiency |
Total |
|||||
|---|---|---|---|---|---|---|---|
Weight |
0.3 |
0.7 |
|||||
Value |
Norm Score |
Weight Score |
Value |
Norm Score |
Weight Score |
||
Option A |
$600 |
1 |
95.13% |
0.959 |
|||
Option B |
$1500 |
0.4 |
99.19% |
1.000 |
We also know that the cost and efficiency weights should be updated to 0.3 and 0.7, respectively.
Unknowns:
Weighted scores for each option
Total score for each option
What is the best solution?
Assumptions: None.
Plan: We need to use the provided weights to calculate new weighted and total scores for the decision matrix. Since we did this in the previous example problem, the calculations are left as an exercise for the reader. We will jump straight to the answers.
Solve: We have the new decision matrix as:
Cost |
Efficiency |
Total |
|||||
|---|---|---|---|---|---|---|---|
Weight |
0.3 |
0.7 |
|||||
Value |
Norm Score |
Weight Score |
Value |
Norm Score |
Weight Score |
||
Option A |
$600 |
1 |
0.300 |
95.13% |
0.959 |
0.671 |
0.971 |
Option B |
$1500 |
0.4 |
0.120 |
99.19% |
1.000 |
0.700 |
0.820 |
Answer: When we compare the scores, we find that Option A is still the best choice.
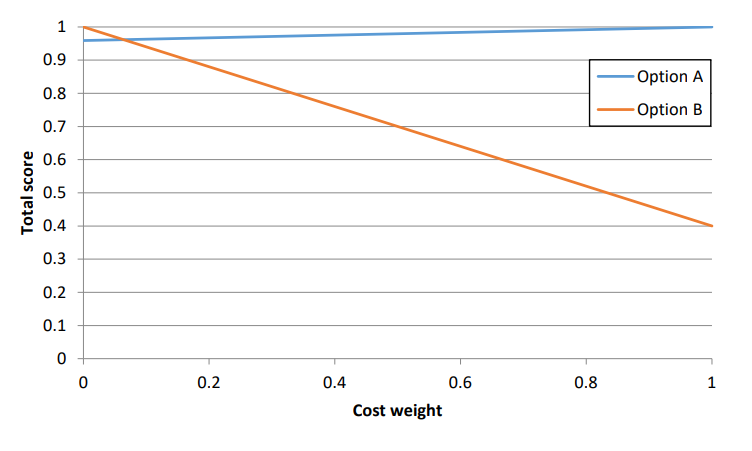
Our use of normalized scores and weighted scores kept us from assuming that the more efficient system was automatically the best choice. If we do some more calculations (as shown in Figure 1 below), we find that Option B won’t be chosen until we assign a weight of 94% to efficiency and 6% to cost! The difference in efficiency from option A to option B is small, but if you plan to run this system for 50 years, the cost savings may become that important!
Engineering Notation#
In this class, you may see an answer in the following form: 810 mW. In case you didn’t know, mW means milliwatts, which means thousandths of a watt. Therefore, 810 mW means 810 thousandths of a watt, or 0.81 W. When we use terms like milliwatts, kilovolts, or gigahertz, we are using engineering notation, which helps to more clearly communicate the values in an engineering problem. If you are familiar with scientific notation, then you have a good start for understanding engineering notation. The basic format of scientific notation is:
\[a \times 10^{b}\]In this format, the variable a (called the coefficient) must be somewhere between 1 and 9.999…. In other words, you get a single digit (from 1 to 9) before the decimal point, and as many digits as you need after it. The variable b (called the exponent) can be any positive or negative integer (including 0). Therefore, if you have a lightning bolt with 825,300,000,000 watts of peak power, scientific notation says we have 8.253 × 1011 W. If the lightning bolt lasts for 0.0001975 seconds, we could write this as 1.975 × 10-4 s. In scientific notation, the exponent simply keeps track of the decimal point. If we move 11 places to the left, then we have 1011. If we move 5 places to the right, then we have 10-5.
Engineering notation is similar to scientific notation, but with two main differences. First, the exponent must always be a multiple of 3.
Fortunately, you already know how to do this for larger numbers. If you wanted to write the power of this lightning bolt, you would never write it like this: 825300000000 W. Even though it’s the right number, it’s not very useful because it too difficult to understand with all of the digits crammed together. Instead, you would use commas to make the number more readable: 825,300,000,000 W. Without even trying, we now know the power of the bolt is hundreds of billions of watts. And that’s what engineering notation does for us. It helps us to intuitively understand the magnitude of the values we’re using.
For large numbers, we can use the commas to figure out where the decimal point goes. What we want to do is replace the first comma with the decimal point.
For our lightning bolt, the first comma falls between the 825 and the 300, which means we have to shift the decimal point 9 places to the left. This means our exponent is 9. Therefore, the peak power is 825.3 × 109 W.
Notice that the coefficient can range from 1 to 999.999…. In many real-life applications, it is common practice to use the range of 0.1 to 9999. For example, you would list a hairdryer as 1200 W, not 1.2 kW. However, in this class, we require that all coefficients range from 1 to 999.999 for final answers. Remember this as it will save you points on the graded events.
The second difference between engineering and scientific notations is the use of prefixes. Once we figure out what the exponent should be, we replace the entire exponential term with a single- letter prefix.
The following chart lists all of the prefixes we will use in this course, which can also be found on your equation sheet:
Prefix |
Symbol |
Power |
|---|---|---|
tera |
T |
10^12 |
giga |
G |
10^9 |
mega |
M |
10^6 |
kilo |
k |
10^3 |
milli |
m |
10^−3 |
micro |
µ |
10^−6 |
nano |
n |
10^−9 |
pico |
p |
10^−12 |
femto |
f |
10^−15 |
atto |
a |
10^−18 |
From this chart, we see that 109 is represented by the prefix giga, or G. Therefore, the value 825.3 × 10^9^ W becomes 825.3 GW.
There are two exceptions. First, distances over 1,000,000 meters (m) are still usually expressed in terms of kilometers (km). Second, lengths between 0.010 and 0.999 m can be expressed in millimeters (mm) or centimeters (cm). One centimeter is a hundredth of a meter, meaning there are 10 mm to 1 cm and 100 cm to 1 m.
Important Note: We will be using engineering notation almost exclusively in this course, and we expect you to use it as well. Towards this end, we recommend you figure out how to put your calculator in engineering mode, so it can shift the decimal point for you. Ask your instructor for help, if needed.
So how do we convert 0.0001975 seconds (s) to engineering notation?
One technique is to add commas, like we did for larger numbers. If we write the duration of the lightning bolt as 0.000,197,5 s, we can see what needs to be done: we recognize that we need to replace the second comma with the decimal point. This means the decimal point needs to shift 6 places to the right, so our exponent is -6. The answer is therefore 197.5 × 10-6 s, which we write as 197.5 µs.
Example Problem 3: A transformer allows us to step up the voltage in a power line while stepping down the current. If the voltage is 43,175 V and the current is 0.00096 A, write these values in correct engineering notation.
Understand: We need to convert numbers in standard notation to engineering notation.
Identify:
Knowns: We have a known voltage and current of 43,175V and 0.00096A, respectively.
Unknowns: We need these quantities in engineering notation.
Assumptions: None.
Plan: Convert to engineering notation by following the rules set out above.
Solve: Hopefully, you quickly realized the voltage is 43.175 kV, since the comma has done most of the work for us. We need to move the decimal point between the 43 and the 175, which means we need to move it three places to the left, which means the exponent is 3. The voltage is therefore 43.175 × 103 V, which we write as 43.175 kV.
Please realize, however, that this is not yet a good engineering answer. The problem is that there are too many significant figures. In this class, unless we explicitly state otherwise, we will expect you to use 3 significant figures. Therefore, the final answer is 43.2 kV.
If we use the comma technique for the current, we get 0.000,96 A. At this point, a few of you might be tempted to say the current is 96 µA, but that would be wrong. What we really need is to add a few trailing zeros (which cost nothing, by the way). Using commas and trailing zeros, the current is, 0.000,960,000,000 A.
Hopefully, you can see that we need to move the decimal point to the second comma, which is 6 places to the right. Therefore, the current is 960 × 10-6, or 960 µA. Notice that this could also be written as 0.960 mA, retaining three significant digits.
Answer: 43.18 kV, 960 µA
Learning Excel#
Excel is a valuable time-saving tool that can be used in the ECE 315 projects and is used extensively throughout the Air Force. If you do not have any experience with Excel, it would be greatly beneficial for you to find a classmate to help you learn or to search online for tutorials.
There are many great resources out there to help you out.
