Lesson 16 – Complex Math#
Learning Outcomes#
Articulate the relationship between imaginary numbers, real numbers, phase angles, and the unit circle.
Demonstrate conversions between rectangular, polar, and phasor forms of a complex number.
Understand how capacitors and inductors work in a circuit.
Complex Math#
Earlier in this course, we introduced the concept of AC circuits and how they differ from DC circuits. As you may have already gathered, the changing voltage and current in AC circuits makes them a bit more complex to design and analyze than DC circuits; however, many technologies we take for granted, such as our efficient power transmission system and communications systems, would not be possible without AC circuits. In this lesson, we are going to build on the math needed to handle more advanced AC circuits and introduce some additional types of electrical components.
First, we need to point out that not all electrical components have the same voltage-to-current ratio for all time. What do we mean by this? To clarify, let’s look at an electrical device we know well at this point, the resistor. The voltage-to-current ratio for a resistor can be fully explained by Ohm’s Law (\(V = IR\)), meaning the ratio between the voltage and the current will always be equal to the resistance, \(R\). No matter how much the voltage or current changes, they will always related to one another according to Ohm’s Law. Some electrical components do not have such a simple relationship between their voltage and current. In fact, many of the electrical systems you use on a daily basis include components that output a different voltage or current depending on how the current or voltage change. These components are primarily known as inductors and capacitors. We use these components to affect how the circuit reacts to certain inputs, and for this reason, we refer to them as reactive components. We choose the size of reactive components based on a few needs: the size of the circuit and the frequencies we need to work with. The voltage and current values for reactive components vary with respect to time, meaning solving for the voltage and current in circuits with reactive components requires solving differential equations. However, by using complex math and only analyzing these circuits at their steady state (i.e. normal operating conditions), we can solve for the voltage and current in these circuits without solving any differential equations.
The easiest way to analyze these components is to leave the time domain and enter the frequency domain. While this sounds scary, it’s actually relatively simple. Before we do this, we will need to introduce a few concepts such as imaginary numbers, the complex plane (for visualization purposes), phasors, and Euler’s identity.
Many of you may recall imaginary numbers from your second level algebra class or your trigonometry class. Recall the definition of the imaginary number (in this class, we’ll use the symbol j, but you’ve probably seen it as i):
This is an important concept even though, by the normal definition, a negative number under the square root does not exist. Often, in the world of electrical engineering, we can simplify our analysis of circuits with reactive components by using these so-called imaginary numbers. Just because an imaginary number is attached to the current or voltage does not mean the voltage or current is “imaginary”. The voltage or current flowing through the component is very real – it is just being used to store energy in a reactive component in the circuit.
Let’s do a little review of some of the properties of j:
We can combine together both “real” numbers and “imaginary” numbers to create “complex” numbers. Consider the complex-plane graph in Figure 1, where we have plotted the complex number 4 + j3. Here, 4 is the “real” part and is plotted on the x-axis, while j3 = 3\(\sqrt{- 1}\) is the “imaginary” part and is plotted on the y-axis. Any number—real, imaginary, or complex—can be similarly located on the complex plane. This give us a way to visualize how these numbers relate to each other and change over time.
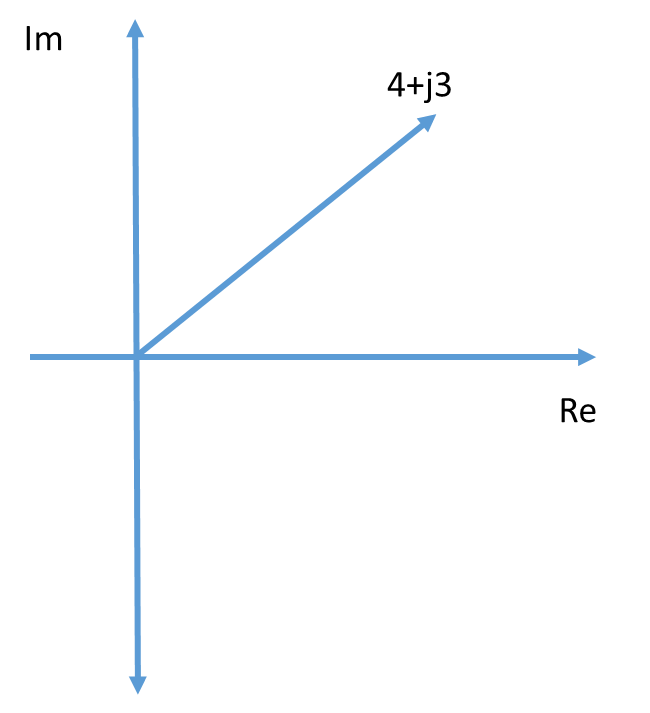
Figure 1: A number graphed on the complex plane
We will see more in the next lesson how j calculations work into circuit analysis. For now we will examine the relationship between the time domain and the frequency domain. In earlier lessons, we learned how an electrical signal can be mathematically expressed by the following expression:
where:
Vm = amplitude of the signal
f = frequency of the signal in Hz
\(\phi\) = phase shift
While this expression describes the signal in the time domain, the time domain isn’t always the easiest way to analyze electrical circuits. Fortunately, we have a way to more easily analyze these circuits. We do this through a mathematical expression called Euler’s Identity. We will not derive Euler’s identity in this class; we will simply use it. Euler’s Identity is used to convert between various forms of complex numbers: rectangular form and polar (phasor) form.
Rectangular |
Polar |
Phasor |
|---|---|---|
\(Acos\phi + jAsin\phi\) |
\(Ae^{j\phi}\) |
A \(\angle\phi\) |
Here, A is the magnitude and \(\phi\) is the angle of the complex number. (The angled bracket denotes “angle”.) These different forms are equivalent, but one or the other may be more useful in a given situation. We will see in the next lesson how this is useful in analyzing circuits.
Example Problem 1#
Convert the following complex number from polar form to rectangular form and phasor form.
Understand: We want to convert from one form to another.
Identify Key Information:
Knowns: The polar form of the number is \(5e^{j{36.87}^{\circ}}\).
Unknowns: The rectangular and phasor form of the number.
Assumptions: The angle is given in degrees, not radians.
Plan: Use the equivalent forms given by Euler’s Identity to convert the polar expression to the two required forms (rectangular and phasor).
Solve: First, we can convert to rectangular form. From the table above, we see the rectangular form as \(Acos\phi + jAsin\phi\) and the polar form as \(Ae^{j\phi}\). By inspection, we can write the rectangular form from the polar form.
Similarly, we can convert from polar form to phasor form by inspection:
Answer: The polar number \(5e^{j{36.87}^{\circ}}\) can be represented in rectangular form as 4+j3 and in phasor form as \(5\angle{36.87}^{\circ}\).
Note that this number is the same one as plotted in Figure 1. In fact, if you measured the angle from the Real axis (x-axis), you would measure exactly \({36.87}^{\circ}\)!
Example Problem 2#
Convert the complex number 3+j4 from rectangular form to polar and phasor form.
Understand: We want to convert from one form to another.
Identify Key Information:
Knowns: The rectangular form of the number is 3+j4.
Unknowns: The polar and phasor form of the number.
Assumptions: The angle is given in degrees, not radians.
Plan: Use trigonometry to convert from rectangular to polar and then convert from polar to phasor by inspection.
Solve: First, we can convert from rectangular to polar form. By a little trigonometry, we find the polar parameters:
Where Re is the real part of the rectangular number and Im is the imaginary part of the rectangular number. Therefore, we have:
So we can write the polar and phasor forms as:
\(Ae^{j\phi} = 5e^{j{53.13}^{\circ}}\) and \(A\angle\phi = 5\angle{53.13}^{\circ}\)
Answer: The rectangular number 3 + j4 can be represented in polar form as \(5e^{j{53.13}^{\circ}}\) and in phasor form as \(5\angle{53.13}^{\circ}\).
Complex Arithmetic#
Basic operations with complex numbers are fairly straightforward, but can also be handled by using your calculator. (Please see the appendix to this lesson and take the time to learn how to use your calculator to do complex math.)
For addition and subtraction, simply add or subtract the real and imaginary parts. This is easiest when the number is in rectangular form. Given two complex numbers, \(Z_{1}\) and \(Z_{2}\), add and subtract the numbers as shown below.
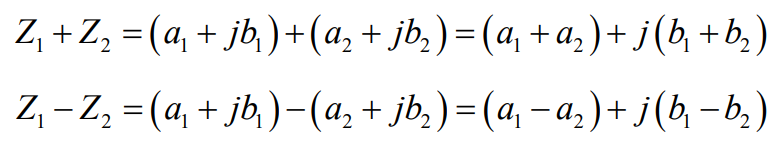
For multiplication and division, multiply or divide the magnitudes and add (multiplication) or subtract (division) the phases. Multiplication or division of complex numbers is easiest when the complex number is in polar or phasor form. Given two complex numbers, \(Z_{1}\) and \(Z_{2}\), multiply and divide the numbers as shown below.
Example Problem 3#
Answer the following problems, giving the answers in rectangular form:
(2+j3) + (3+j4)
(2+j3) * (3+j4)
(5+j5) – (3-j6)
(2+j3) / (3+j4)
Understand: We are just reviewing complex math and conversion from one form to another.
Identify Key Information:
Knowns: The rectangular form of the numbers.
Unknowns: The final answers.
Assumptions: The angle is given in degrees, not radians.
Plan: Use the complex math rules set out above, converting to the proper form when necessary. Verify using our correctly configured calculator.
Solve:
(2+j3) + (3+j4) = (2+3) + j(4+3) = 5+j7
(2+j3) * (3+j4) = \(\left( \sqrt{2^{2} + 3^{2}}\ \angle\arctan\left( \frac{3}{2} \right) \right)*\left( \sqrt{3^{2} + 4^{2}}\ \angle\arctan\left( \frac{4}{3} \right) \right)\)
= \(\left( 3.61\ \angle{56.31}^{\circ} \right)*\left( 5\angle{53.13}^{\circ} \right)\)
\(= (3.61*5)\ \angle({56.31}^{\circ} + {53.13}^{\circ})\)
\(\ = 18.05\ \angle\left( {109.44}^{\circ} \right)\)=
(5+j5) – (3-j6) = (5-3)+j(5+6) = 2+j11
(2+j3) / (3+j4) = \(\left( \sqrt{2^{2} + 3^{2}}\ \angle\arctan\left( \frac{3}{2} \right) \right)/\left( \sqrt{3^{2} + 4^{2}}\ \angle\arctan\left( \frac{4}{3} \right) \right)\)
= \(\left( 3.61\ \angle{56.31}^{\circ} \right)/\left( 5\angle{53.13}^{\circ} \right)\)
\(= \left( \frac{3.61}{5} \right)\angle{(56.31}^{\circ} - {53.13}^{\circ})\)=0.722\(\ \angle{3.18}^{\circ}\)
Now that we can do the math, let’s look at the components which drive the math: capacitors and inductors. They can be useful for all sorts of things, but especially for creating filters to get rid of unwanted signals.
Capacitors#
Capacitors store electric energy in a circuit. A capacitor is made of two conductive plates separated by a dielectric medium. When the circuit is energized and current is flowing, the dielectric medium keeps the charges separated – positive charges go to one plate, and negative charges go to the other. The charges on one plate are now attracted to the charges on the other plate which is how a capacitor stores energy. The capacitor stores this energy in the form of an electric field.
A capacitor is symbolized in a circuit as shown below:
Figure 2: Capacitor symbol
The units for a capacitor are Farads, named after Michael Faraday, a British electrochemist. Capacitance, or Farads (F), are really Coulombs/Volt. A Coulomb is the unit for charge and a volt is the potential difference between two points. This makes a Farad the amount of charge stored per volt of potential difference. Most capacitors are rated in the 10^-6^ or microFarad (µF) range, which is clearly very small!
Because a capacitor doesn’t charge instantaneously, it is a reactive element, meaning the voltage or current reacts to changes in the other variable. For a capacitor, the current only exists if the voltage is changing. This can be seen in the equation below.
This is an ordinary differential equation. A quick look at it tells us that current only flows when a voltage is changing across the parallel plates of the capacitor and that the current is proportional to how quickly the voltage is changing across the capacitor. This concept helps explain why many systems don’t respond instantaneously when you push a button – those buttons have capacitance (and, often, inductance) which take time to charge. Also, you have probably experienced a similar phenomenon when you unplug your AC adapter from the wall – the LED light continues to glow for a short time while the elements inside discharge their current. Also, take note that capacitors don’t “like” large changes in voltage. For example, if the voltage changes a large amount over a very short time, the time derivative of the voltage (\(\frac{\partial V}{\partial t}\)) goes to infinity, which results in a very large current. The following graph gives an idea of how voltage builds up within a capacitor over time, which is a function of charge accumulating at each of the plates within the capacitor.
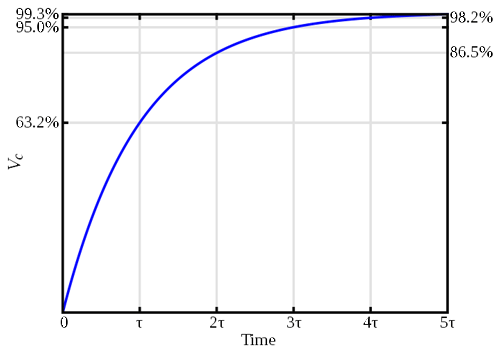
Figure 3: Voltage buildup on a capacitor over time
You can see, as time goes on, the capacitor will reach what is called “steady state” which occurs when the capacitor is fully charged. There is an easier way to model a capacitor when you are acting in a steady state system – the system receives an input and has a chance to “work through” this transient part of the signal. At this point, we can use complex math to treat the capacitor in a manner similar to a resistor, which we will discuss next lesson.
Inductors#
The other reactive electrical component we will study is the inductor. An inductor is, quite simply, a coil of wire around a core, which is typically made of air or metal. The coil creates a magnetic field when a current is passed through it. While a capacitor does not like large changes in voltage, an inductor does not like large changes in current. The inductor tries to conteract changes in current by setting up a magnetic field within its coils. This is how an inductor stores its energy. Once power is removed from an inductor, the magnetic field collapses and no energy is stored. Unlike a capacitor, you never need to discharge an inductor – it will discharge itself!
An inductor is represented in an electrical circuit as shown below:
Figure 4: Inductor symbol
The unit for an inductor is the Henry, abbreviated H. However, when used in an equation, an inductor is represented by a capital L. Just like capacitors, inductors vary their electrical parameters with respect to time. This time the relationship is:
This states the voltage across the inductor is equal to the inductance times the change in current with respect to time. In this case, conversely to the capacitor, inductors don’t “like” sudden changes in current, because they result in very large voltages. Also, just like with a capacitor, once an inductor reaches steady state, complex math can be used to treat it like a resistor, which we will discuss next lesson.
Appendix: Using the Casio fx-115ES PLUS to Calculate with Complex Numbers#
Get your calculator set up for Engineering calculations in complex mode.
a. This is not a mandatory step, but there could be some interaction between settings you have made previously and the following directions. Therefore, I recommend completely resetting the calculator and returning it to “factory default” settings. To do so, 1) Turn on the calculator by pressing the On button; 2) Press Shift, 9 (CLR), 3 (All), = (Yes); 3) Press the AC key to return to the main screen.
b. Next, set the calculator to complex mode by pressing Mode and then 2:CMPLX. You should see the CMPLX indicator just to the left of center at the top of your screen. If you reset the calculator as described in step 1, you should also see a “D” indicating the units for angles are in degrees and “Math”, which means “natural display” of answers is selected. Natural display means that easily reduced fractions will be displayed as fractions, so 4/3 is displayed as 4/3 rather than 1.333 or some other approximately correct value, and 5/4 is displayed at 5/4 instead of 1.25, which is exactly correct.
c. As you enter calculations, you will see some triangles shown in the upper right side of the display. Pressing the up arrow will take you to older results. The down arrow will take you to the more recent results. If both arrows are shown, both older and newer results available. If only up arrow is shown, you are already at the most recent result and only older results are available. If only the down arrow is shown, you are at the oldest result, and only newer results are available. Entering a new calculation brings you back the newest result leaving the other calculations on the stack. If you think of this as a stack, the oldest things are at the top of the stack and the newest are at the bottom. Note that clearing the memory (SHIFT~9~2~=) does not clear the stack!
d. Although we prefer our answers to be in engineering notation, this calculator does not support that form. The closest form is scientific notation. To put the calculator in scientific notation, press SHIFT~SETUP~7. You will then be prompted for the number of digits you want displayed with one appearing before the decimal point and N-1 after. If you are still in Math mode, some numbers might be displayed as fractions. To display everything in scientific notation, press SHIFT~SETUP~2:LineIO.
e. The last step is to set up the default display of complex numbers. You have two choices:
i. Rectangular -- numbers are displayed with a real and an imaginary part (e.g., 3+4i) ii. Polar, which means numbers are displayed with a magnitude and angle. Most of the time, answers are more useful in polar form. To get polar form by default, press SHIFT-SETUP and then the down arrow on the REPLAY button. Option 3 will be CMPLX so press 3 and you will see the two options. To display results in polar form press $\ 2\ :r\angle\theta$ .
