Lesson 11 – Power Distribution#
Learning Outcomes#
Understand how electrical busses provide voltage and current to all connected devices.
Given a power distribution system with AC and DC busses, calculate the required transformer turns ratio between electrical busses and determine appropriate values for circuit breaker protection.
Solve for the power provided by a source, the power consumed by various devices, the current at various points, and the efficiency of a power distribution system
Power Distribution#
Power distribution is the process of getting power where it needs to go. It can involve getting electricity from a power plant to a community as we discussed in the previous lesson, or it can provide the appropriate power to every electrical component on an airplane.
As systems become more and more complex, trying to draw the circuit in the traditional way accurately can become both tedious and confusing. For this reason, engineers often use simple block diagrams to capture the essence of electronic systems.
Consider the following representation of a part of the T-52 electrical system in Figure 1:
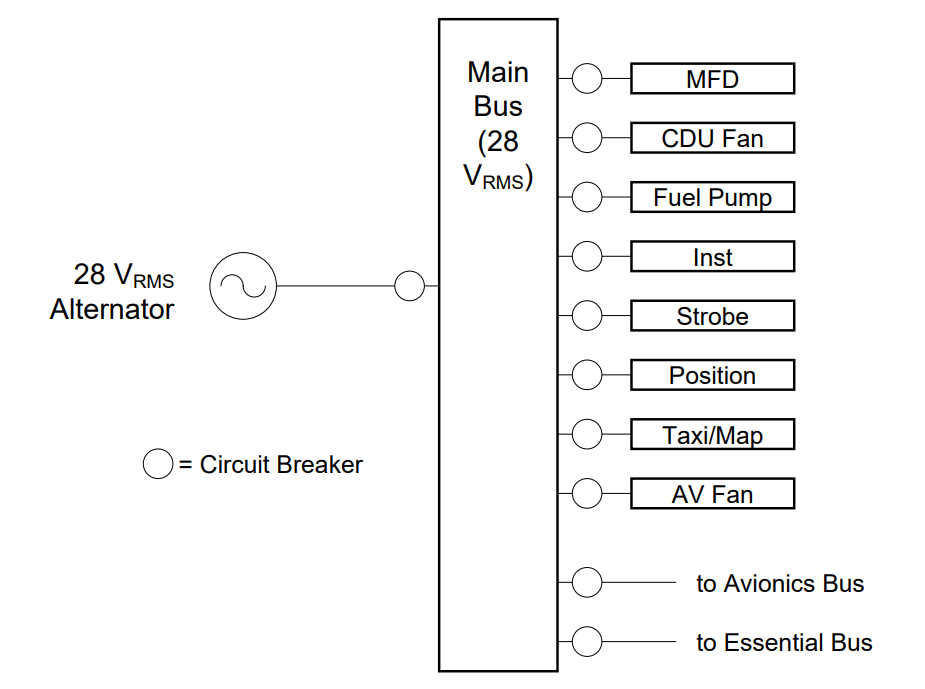
Figure 1: The power bus of a T-52
On the right of this diagram, we see eight components (MFD, CDU Fan, etc.) which require 28 VRMS to operate (don’t worry about what the components actually are – we don’t need to know in order to model the power flow of the system). These items receive 28 VRMS from the Main Bus which gets 28 VRMS from the alternator*.* An alternator is a type of generator mostly used to generate power from automotive and other internal combustion engines. Notice, in the block diagram, the Main Bus also provides 28 VRMS to two other busses, an Avionics Bus and an Essential Bus. Also notice how every device in the system, including the busses themselves, is protected by circuit breakers. This is just good engineering practice.
Key concept: Electrical buses provide power to devices connected in parallel between the bus and a common ground. All devices connected to a bus receive the same voltage.
A bus is simply a piece of metal or wiring which has a known voltage applied to it. To explain what this means, let’s look at the equivalent circuit diagram (Figure 2) for the same portion of the T-52 electrical system:
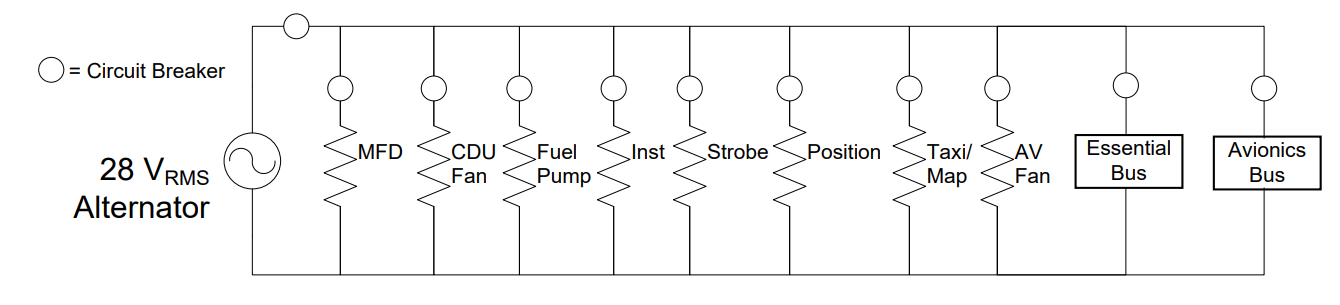
Figure 2: The traditional circuit diagram for a T-52 electrical system
It is important to realize both of the above diagrams are equivalent since they both convey the same amount of information about the electrical system. They just do it differently.
Since all of the devices (including the Essential and Avionics Busses) require the same voltage, we put everything in parallel with the voltage source (the 28 VRMS alternator). Hopefully, this makes sense, since devices in parallel share the same voltage and we want everything to share 28 VRMS. If we added anything else to the bus, it would also be added in parallel and would therefore get the full 28 VRMS dropped across it. But where is the Main Bus in this circuit diagram? The bus is simply the upper node of the circuit, as in Figure 3:
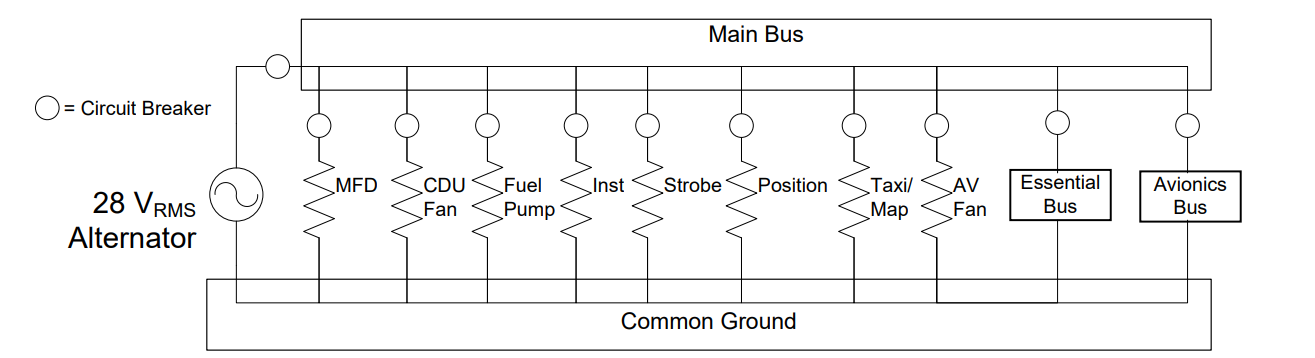
Figure 3: T-52 Circuit Diagram
Many electrical systems, including our homes, will use a metal bar (Figure 4), to serve as a bus. Any device that is added to the bus is simply wired directly to this metal bar. As long as everything is wired in parallel, all devices get the expected voltage.

Figure 4: Metal bar serving as a bus
(Source: http://www.vonwentzel.net/Prout/02.Electrical/08.Wiring/)
We often talk about a bus (or a node) as having a specific voltage, such as saying the T-52 Main Bus has a voltage of 28 VRMS. While this is very useful, it is not technically accurate. What we really mean is the voltage drop from the bus to a common ground is 28 VRMS. Just as a bus is a common node used to provide a common voltage to different devices, a common ground is also a common node used to return the current flow back to the source. The circuit diagram above shows the common ground as the lower node in the circuit. In the block diagrams, the common ground, which completes the circuit(s) is implied but not shown.
Most vehicles, such as cars and airplanes, actually use the metal frame of the vehicle to serve as a common ground. Therefore, adding electrical devices is as simple as running a wire from the appropriate bus to provide power, and then grounding the device to the metal frame to provide a return path back to the battery or generator. This is why many of you have been taught to clamp the black jumper cable to the charging car’s chassis - this is the safest way of making sure you have the circuit grounded!
If we define the common ground to be zero volts, then all other voltages can be given with respect to this value. Therefore, when we say the Main Bus has 28 VRMS, what we really mean is that it has a voltage that is 28 VRMS higher than the common ground. This same principle is true with the electrical power we receive from our wall outlets. We say we get 120 VRMS from a wall outlet, but what we really get is a voltage that is 120 VRMS higher than the common ground running through our house.
Circuit Protection#
When designing an electrical distribution system, many will ask the question: “How many breakers do you need?” The answer to that question varies greatly depending on what is being connected. Some systems may only need a couple breakers for the whole system. Others may need them hooked to many components. For example, if you were designing an electrical system for an aircraft with numerous vital systems (such as flight controls, radar, communication systems, etc…) hooked to the same bus, would you want to put one breaker/fuse on the front end of that bus? What would happen if the radar system shorted out? The answer is that the one breaker/fuse would shut off all systems hooked to that bus, causing all your vital systems to fail instead of just the radar. Not a good thing. Therefore, gauge the number and location of your breakers/fuses according to the design.
Another salient question is how we should size the fuses and/or circuit breakers. This is more art than it is science, but a good heuristic is 10-15% above the max current draw. This gives the circuit some “headroom” to allow for small transient signals, while still protecting sensitive components. In the real world, fuses and breakers come in predefined ratings, so you would choose the closest appropriate value from the available fuses or breakers.
Example Problem 1:#
An aircraft power system is to be powered by a 190 VRMS generator. Design the power distribution system for this airplane to meet the following requirements:
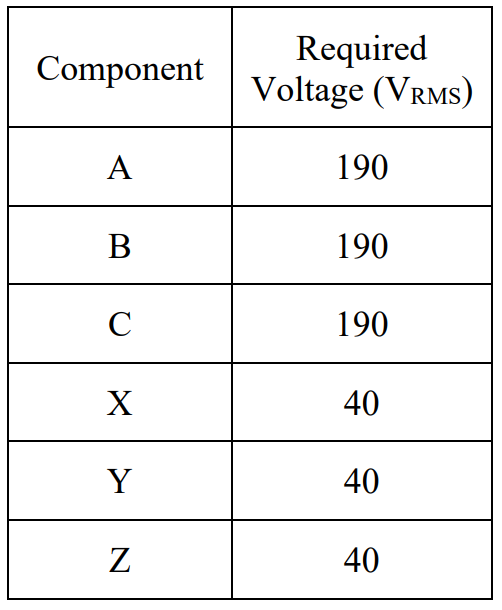
Understand: Since the requirements dictate two different voltages, we will need a transformer at some point in the design. Otherwise, we need to ensure each component is connected to the appropriate bus for its required voltage.
Identify Key Information:
Knowns: We know the voltage required for each component.
Unknowns: The layout of the system and the turns ratio for the transformer (a).
Assumptions: None.
Plan: We will draw an initial block diagram, and calculate the turns ratio of the transformer based on the RMS values of the bus voltages.
Solve: Here’s a preliminary block diagram of the required power distribution system:
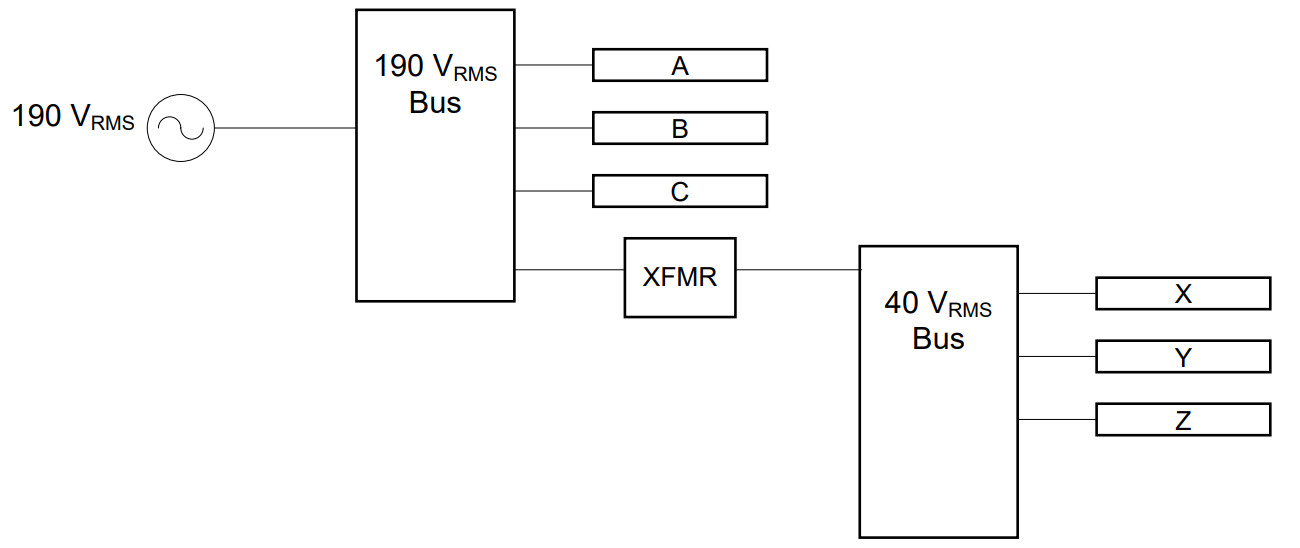
The devices A, B, C, X, Y, and Z are added merely to show how various devices are connected to each bus. The 190 VRMS bus receives power from the generator and distributes this power to devices A, B, and C, and also to a transformer. The transformer steps the voltage down to 40 VRMS and sends the dropped-down voltage to the 40 VRMS bus, which in turn provides power to devices X, Y, and Z.
The only thing that needs to be done is to calculate the turns ratio of the transformer. Using the turns ratio equation gives us:
Answer: The aircraft power distribution system can be implemented as shown above, where the transformer has a turns ratio of a = 4.75.
Although that seems straightforward, we haven’t talked about current draws and power dissipation for these systems. Thankfully, since the components are all connected in parallel, analyzing current draws and power dissipation is relatively simple. We know the voltage drops are all the same and the current provided by the source (or entering the common bus node) equals the currents distributed between the individual devices (or exiting the common bus node). In our T-52 example (Figure 5), the current drawn from the 28 VRMS alternator would be equal to the sum of the current draws from the MFD, CDU Fan, Fuel Pump, etc. plus the total current draws of the Essential Bus and Avionics Bus. Also, since we have assumed there are no power losses in the lines, the power the source must deliver is equal to the sum of the power dissipated by the individual components and additional buses.
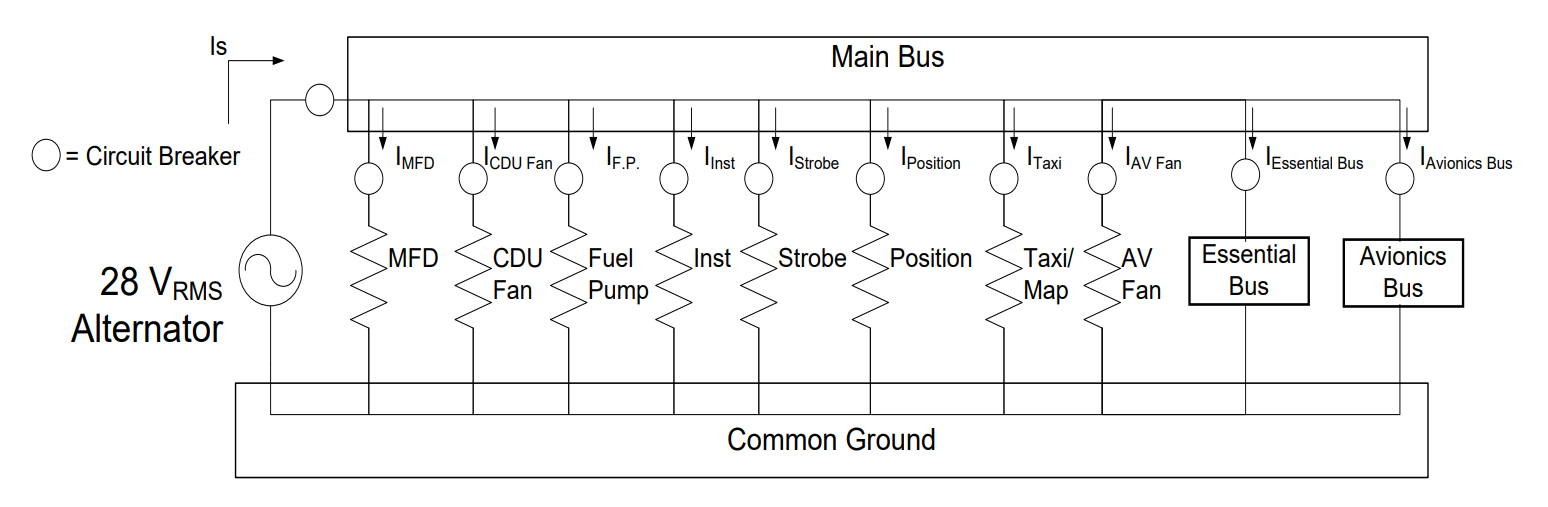
Figure 5: T-52 bus example
Example Problem 2:#
Add circuit protection to the following aircraft power system given the following component current draws. Also, calculate how much power the generator must provide to drive all of the components on the two buses.
Device |
Voltage (Vrms) |
Current (Arms) |
|---|---|---|
A |
190 |
3 |
B |
190 |
8 |
C |
190 |
3 |
X |
40 |
10 |
Y |
40 |
4 |
Z |
40 |
5 |
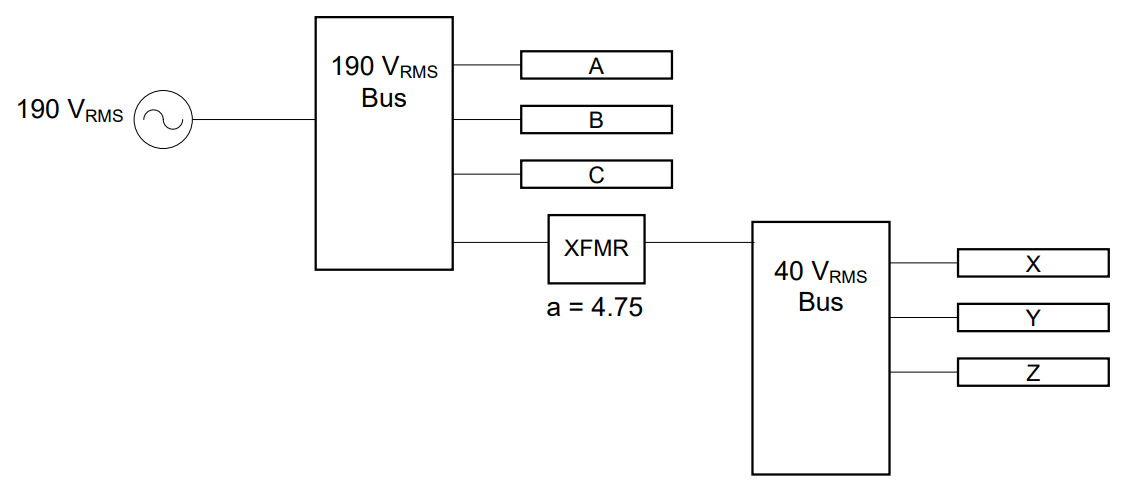
Understand: The key to circuit protection is to figure out the flow of currents in the system. Since we can consider a bus to be the same thing as a node, the total current flowing into the bus will be equal to the total current flowing out of it. We are building upon the design of the previous
Identify Key Information:
Knowns: We know the required voltages and currents for all loads, the transformer turns ratio
Unknowns: The total current draw of the generator, the power it supplies to the system, and the locations for circuit breakers.
Assumptions: None.
Plan: First, we have already designed the system to ensure the appropriate voltage is provided to each component. Next, we need to determine the current flow through each bus, which will give us the current provided by the generator. Finally, since we know the current and voltage of the generator, we can determine the power supplied by the generator.
Solve: Let’s look at the currents into and out of the 40 VRMS Bus first, using the values from the table above:
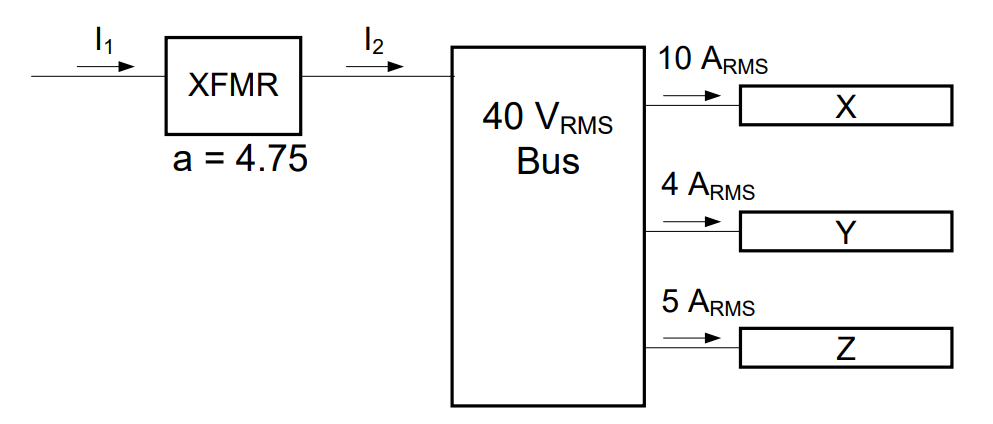
Using the KCL equation, we recognize the total current into the bus is the total current out of the bus:
Therefore, the current coming from the transformer to the 40 VRMS bus is 19 ARMS. We can now use this current in the turns ratio equation to determine the current coming into the transformer:
Therefore the transformer steps the voltage down from 190 VRMS to 40 VRMS and it steps the current up from 4 ARMS to 19 ARMS. Let’s now look at the currents in the rest of the system:
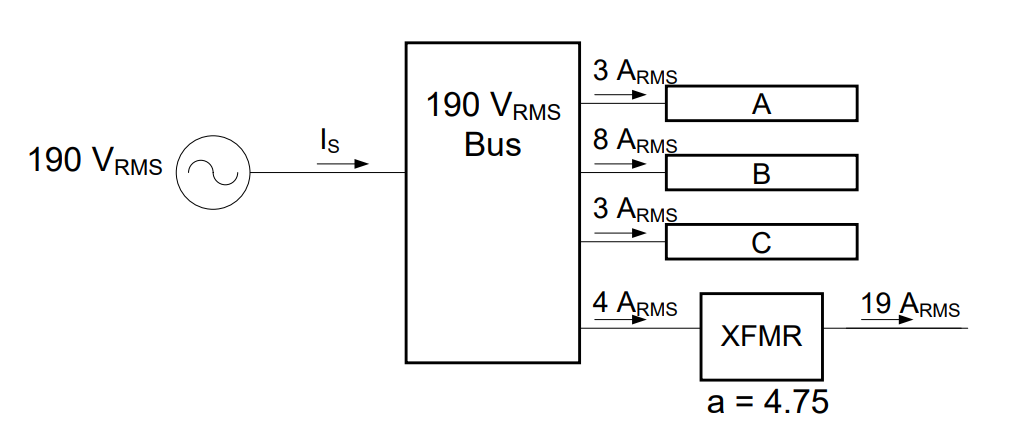
We can solve for the current coming from the source to the 190 VRMS Bus. It is very important to realize only 4 ARMS leaves the bus to go to the transformer.
We now know all the currents in the circuit, and therefore can add the required circuit protection as shown below:
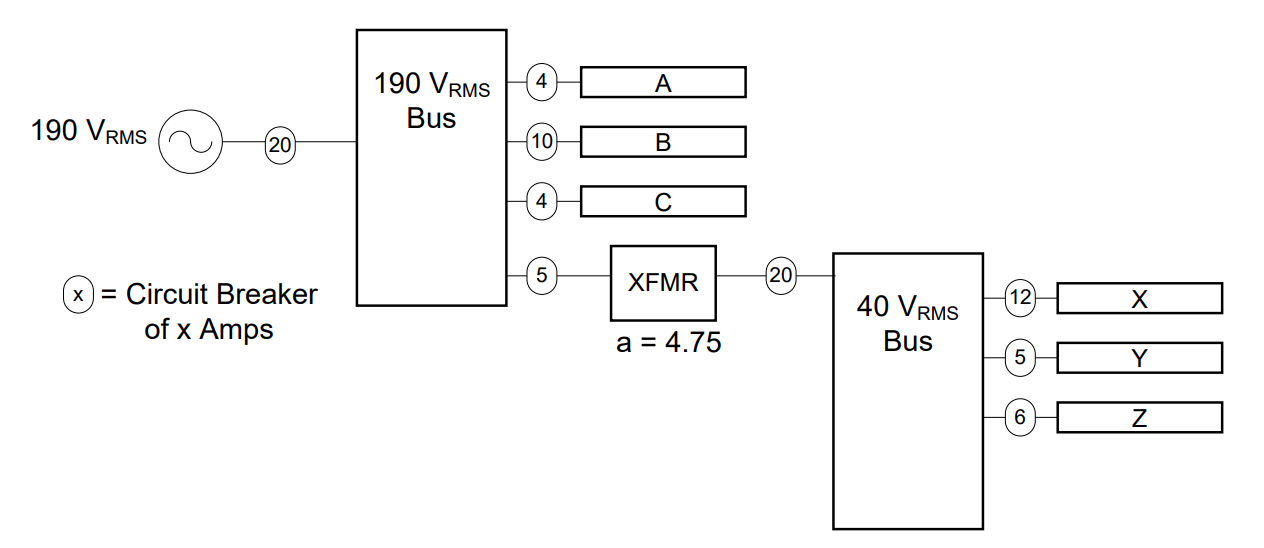
Because we are adding circuit protection, the circuit breaker ratings are all selected so that normal current draws will never cause the breaker to pop open.
The last step is to calculate the power the 190 VRMS system must provide. The easiest way to calculate this is to add up the power draws of each individual component:
Note how the power draw varies significantly between the two busses, based on the voltage of each.
Answer: The power distribution system with circuit protection as shown in the previous diagram must provide 3.42 kW of power.
Example Problem 3:#
An aircraft electrical system consists of a 160-VRMS Bus and a 28-VDC Bus, as shown. Calculate the turns ratio of the transformer and pick acceptable values for the circuit breakers labeled A and B. Assume the Comm and Camera each draw 3 A. The AC-to-DC converter is 90% efficient.
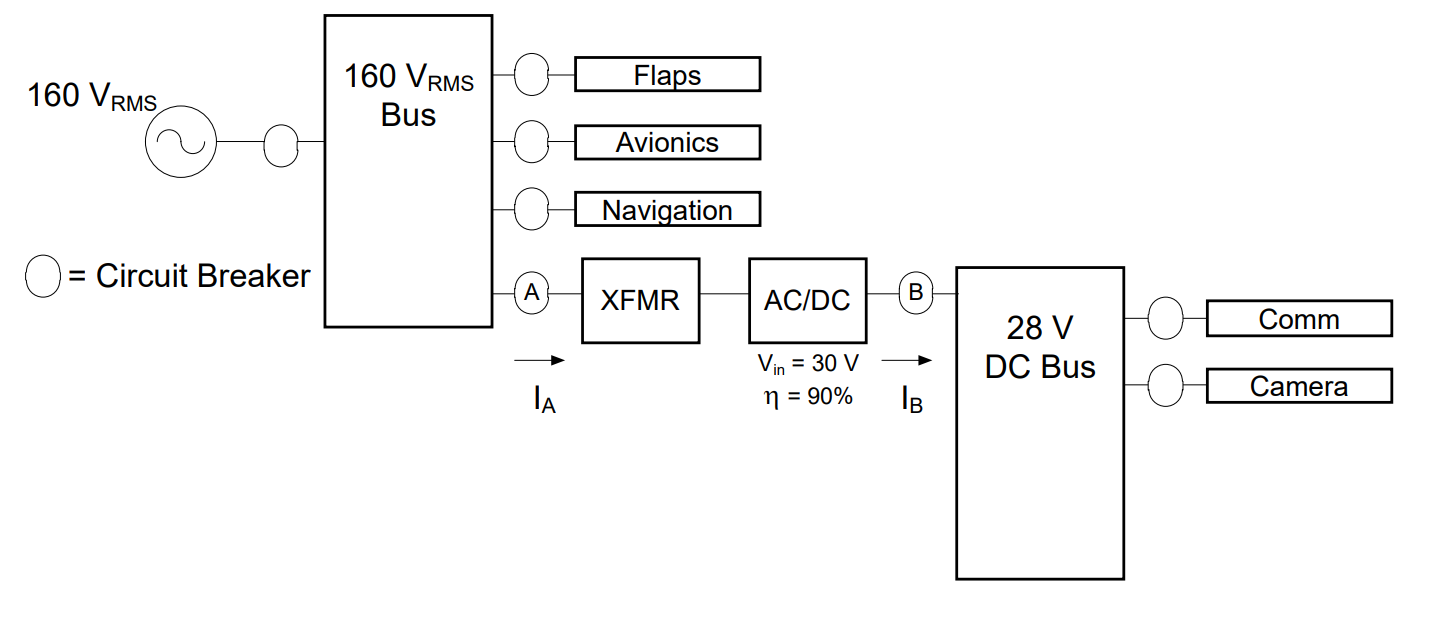
Understand: This example considers the scenario where a DC Bus is required. We will need to solve for power to figure out circuit breaker A.
Identify Key Information:
Knowns: Current required by the loads, bus voltages, AC/DC efficiency, AC/DC input voltage
Unknowns: Circuit breaker values, transformer turns ratio, node currents
Assumptions: None
Plan: This consists of three separate problems, which we will solve separately. First, we will solve for the current through breaker B using KCL, then utilize the efficiency equation and conservation of power across the transformer to determine the current at A.
Solve: We will start by calculating the current through breaker B. Since the DC Bus is really just an electrical node, KCL tells us:
Therefore, we can pick a circuit breaker rating for B that is a little higher than 6 A. We will pick an 8 A circuit breaker.
The next problem is to find the turns ratio for the transformer. If we look just at the AC-to-DC converter (with transformer) portion of the system, we have:

We already solved a problem like this earlier. The key is to realize 30 V is the peak voltage, not the RMS. With transformers you can determine the turns ratio using the peak voltages or the RMS voltage, but it must be consistent. For this example we will convert the 30 V peak voltage to RMS:

Therefore, we will need a transformer with a turns ratio of 7.544.
Finally, we can calculate the current through breaker A. The key to this is to treat this as a power problem and solve for the power consumed by the DC equipment.

For these types of problems, it is usually best to start at the right (the load) and work to the left (towards the source). The DC Bus uses 6 A at 28 V. Therefore, the power consumed by the equipment on the DC bus is
Since this is the amount of power that the AC to DC converter needs to provide,
Now we need to use the efficiency equation to solve for Pin:
Since the transformer consumes no power,
We call this power, PDC\ bus, since this is the total amount of power provided to the 28 VDC bus, including the power lost in conversion. What this means is the 160 VRMS Bus provides 186.7 W of average power to the DC system at 160 VRMS. If we use the power equation, we can solve for current:
Therefore the current through circuit breaker A is 1.167 A. We will choose a 1.5 A circuit breaker to protect the circuit.
Answer: The aircraft power system needs a transformer with a turns ratio of 7.143. The selected circuit breaker values are 1.5 A for circuit breaker A, and 8 A for circuit breaker B.
