Lesson 32 – The Friis Equation

Learning Outcomes

1. Articulate the limiting factors that determine if communication between two locations is possible.

2. Use the Friis and Line-of-Sight equations to calculate the maximum communication distance between a transmitter and receiver.

3. Understand the concepts of signal-to-noise ratio (SNR), receiver bandwidth, and noise temperature.

4. Articulate how the parameters in the Friis and SNR equations affect a communication system’s power budget.

5. Understand the concept of decibels.

Friis Equation

Introduction

Previously, we discussed the four wireless RF propagation methods. We left off with a fairly simple equation to calculate the maximum line of sight (bLOS) range for two communication systems. However, LOS is not the only factor that determines whether or not those two systems can communicate. In fact, just because two antennas are within the maximum LOS range doesn’t mean they can actually communicate. Electrical signals attenuate (become weaker) as they propagate over a distance. If the received signal is too weak, the receiving radio will not be able to detect or process it. In fact, every radio has a certain threshold for received power, or Signal-to-Noise Ratio (SNR), which must be met in order to establish a communications link. The Friis equation provides the means to calculate received power, given a number of attributing factors. If the received power, or the SNR, is above the threshold, and the radios are within the maximum LOS range, they can effectively communicate.

Friis Equation

The equation for determining how much power actually reaches the receiving antenna is called the Friis (rhymes with Greece) equation:

\[P_{R} = \ P_{T}G_{T}G_{R}\frac{\lambda^{2}}{{(4\pi R)}^{2}}\]

where the variables are as follows:

• P­_R­: The power collected by the receiving antenna (in Watts)

• P­_T­: The power sent by the transmitting antenna (in Watts)

• G­_T­: The gain of the transmitting antenna (unitless)

• G­_R­: The gain of the receiving antenna (unitless)

• λ: The wavelength of the radio signal (in meters)

• R: The distance between the two antennas (in meters)

Let’s look at these variables and how they affect the strength of the signal that gets to our receiving antenna.

Power Transmitted, P­_T­: The power transmitted, P­_T­, clearly affects received power. In fact, P­_T­ and P­_R­ are directly proportional, so as P­_T­ increases, P­_R­ also increases.

Distance (or Radius) between Antennas, R: To understand the effect of distance on the amount of received power, consider a point source radiating P­_T­ Watts of power equally in all directions, which is effectively a sphere. At any point on a sphere of radius, R, away from the transmitting point source, we can define the power density, S, in Watts/m^2^, as the total power radiated, P­_T­, divided by the surface area of the sphere, 4πR^2^. That is,

\[S = \frac{P_{T}}{4\pi R^{2}}\]

From this, we see the power density is proportional to \(\frac{1}{R^{2}}\). Soon, we will see the received power, P­_R­, is proportional to the power density. As a result, received power is proportional to \(\frac{1}{R^{2}}\).

Gain of the Transmitting Antenna, G­_T­: The gain of the transmitting antenna, G­_T­, is its ability to focus energy in one direction; therefore, the gain acts as a multiplier of the transmitted power. As a result, the power density, S, on a sphere at a distance, R, in the direction of maximum gain, for any type of antenna is:

\[S = P_{T}G_{T}\frac{1}{4\pi R^{2}}\]

where the gain, G­_T­, is unitless. Therefore, when the receiving antenna is placed in the direction of maximum gain, the power density will also be maximized. We will often rely on this assumption to determine whether two radios can communicate. Since P­_R­ is proportional to S, we see P­_R­ is also proportional to G­_T­.

Gain of Receiving Antenna: The receiving antenna also has a gain, which describes how much energy it collects from the transmitted signal. In order to see how the gain of the receiving antenna affects how much power we receive, recall the transmitted signal propagates through free space in the shape of a sphere. As we get farther and farther from the transmitting antenna, the surface of the sphere starts to appear flat to the receiving antenna – this is called a “plane wave”. This idea is shown in the figure below, and is similar to the perception of a flat earth due to its large radius compared to the limited surface area that we perceive.

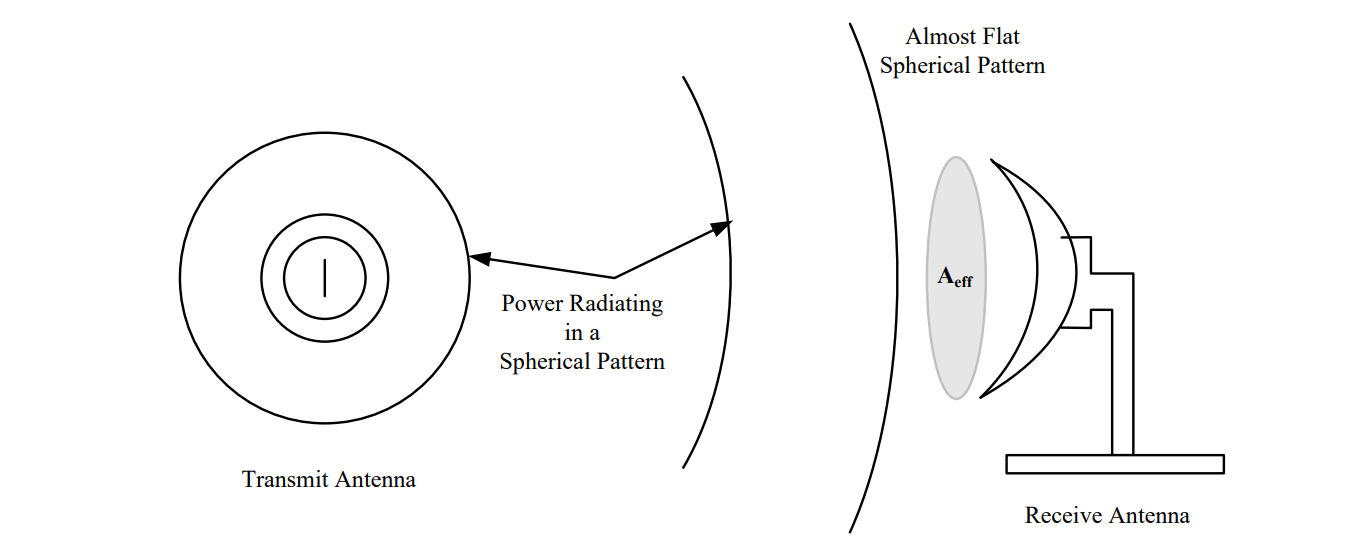
Figure 1: The propagation of a signal from the transmitter to receiver. Note how the spherical wave appears nearly flat at the receiver.

The amount of power the receiving antenna can capture from free space depends on the effective area of the antenna, A­_eff­. Although this can be thought of as the physical size of the antenna, they are not quite the same, as the effective area is actually the size of the antenna relative to the wavelength of the signal and proportional to the inherent gain of the antenna (G­_R­). As an example, parabolic antennas have an effective area that is slightly smaller than their physical area. The power received then is the effective area of the receiving antenna times the power density.

\[P_{R} = SA_{eff} = P_{T}G_{T}\frac{A_{eff}}{4\pi R^{2}}\]

As discussed, the effective area of the receiving antenna is related to the wavelength of the signal:

\[A_{eff} = \frac{\lambda^{2}}{4\pi}G_{R}\]

Substituting this equation into the one above gives us the final Friis equation as introduced earlier,

Key Concept – Friis Equation

\[P_{R} = P_{T}G_{T}G_{R}\frac{\lambda^{2}}{(4\pi R)^{2}}\]

Here is a quick summary of how the variables affect the power received:

• Doubling the transmitted power (P­_T­), doubles the received power (P­_R­).

• Doubling the gain of either the transmitting or receiving antenna (G­_T­ or G­_R­) doubles the received power. If both are doubled, the received power quadruples.

• Doubling the wavelength of the signal quadruples the received power! Doubling the wavelength is equivalent to halving the frequency. Although we have alluded to the fact that lower frequencies travel further than higher frequencies, the Friis equation is the proof. For example, broadcasting a lower frequency means we transmit more power to the receiver.

• Doubling the distance reduces the received power (P­_R­) by a fourth. The strength of an electromagnetic wave is inversely proportional to the square of the distance. This is intuitive, as the farther you are from a transmitter, the weaker the signal is.

When using the Friis equation, your calculator is your friend, but because of the form of the equation, be sure to avoid the following errors:

• Calculating λ incorrectly. If you neglect to include the speed of light, your answer will be off by a factor of 90 x 10^15^.

• Using the wrong distance. Remember that the distance is in meters, not kilometers. Therefore, in the problem below, R = 50,000 m.

• Not squaring the 4 or the π in the denominator.

Example Problem 1

A search and rescue helicopter is at 450’ AGL because of clouds, while the airman they are trying to find is on a 50-foot hill. The airman’s survival radio transmits 6 W of power at 121.5 kHz, and uses an antenna with a gain of 3.0. The helicopter’s radio has a gain of 3.2 and requires a minimum ofs 50 μW of power to receive the transmission. If the helicopter is 50 km away from the airman, will the helicopter crew be able to hear the airman?

Understand: To ensure the helicopter and the airman can communicate, they must have both LOS [and]{.underline} sufficient power.

Identify Key Information:

• Knowns: We know the height of both the helicopter and airman and we know the specifications of each radio. Since these types of problems often have quite a few unknowns, it is useful to write them explicitly as follows:

  Symbol	Value
  h­helo­	450 feet
  h­airman­	50 feet
  f	121.5 kHz
  P­T­	6W
  P­R, min­	50 μW
  G­T­	3
  G­R­	3.2
  R	50 km

• Unknowns: The maximum LOS range and the maximum range based on the minimum power. Note that we are given the minimum power the receiver needs to process the signal. Since the power is at a minimum far away from the transmitter, this will give us the maximum distance the two radios can communicate across.

• Assumptions: The communications link relies solely on LOS and not any of the other means (forward scatter, ground wave, or sky wave). Additionally, we can assume the beams of the transmitting antenna and receiving antenna are aligned such that their maximum gains overlap.

Plan: There are three key steps to this problem:

• First we must calculate the maximum LOS range, based on the heights of each radio. If LOS is established (i.e., the actual range is less than the LOS range), we can move on. Note, we calculate the line of sight in miles, but the distance is given in kilometers. We must therefore convert (use 1 mile = 1.61 km).

• Then, we calculate the received power, using the Friis equation, based on the actual range.

• Finally, we compare the received power to the minimum power that the receiver needs to process the signal.

Solve: First, we calculate the LOS of the helicopter and the airman by:

\[r = \ \sqrt{2h_{helo}} + \sqrt{2h_{airman}} = \ \sqrt{2*450} + \ \sqrt{2*50} = \ \sqrt{900} + \ \sqrt{100} = 40\ miles\]

Converting this distance to kilometers:

\[40\ miles*\ \frac{1.61\ km}{1\ mile}\ = \ \ 64.4\ km.\]

The actual separation of 50 km is well within the 64.4 km maximum LOS range, so LOS is established. Therefore, we can move on to solving for power received.

Before using the Friis equation, we need to find the wavelength:

\[\lambda = \ \frac{c}{f}\ = \ \ \frac{3*10^{8}\ m/s}{121.5*10^{3}\ Hz}\ = 2.469\ km\]

Notice this is a huge wavelength, more than 1.5 miles. Now, using the Friis equation:

\[P_{R} = \ P_{T}G_{T}G_{R}\frac{\lambda^{2}}{{(4\pi R)}^{2}}\ = (6\ W)(3)(3.2)\frac{(2469\ m)^{2}}{(4\pi*50,000\ m)^{2}} = 889\ \mu W\ \]

Since the receiver only needs 50 μW of power, the actual signal is more than strong enough to allow the helicopter crew to hear the airman.

Answer: Yes, the helicopter crew will be able to hear the airman. LOS is established and the power received is 889 μW, which is much greater than the required 50 μW.

Example Problem 2

Two circular parabolic dishes, each with a radius of 250 mm, are used to send a microwave communication signal at 2.7 GHz. Both dishes have an efficiency of 91%. If the transmit power is 1.2 kW, how much power is received if the antennas are 120 km apart?

Understand: We have two parabolic antennas trying to communicate.

We need to first calculate the gain of the two antennas.

Identify Key Information:

• Knowns: We know the following quantities:

  Symbol	Value
  Antenna 1 Radius \((r_{1})\)	250 mm
  Antenna 1 Efficiency \((η_{1})\)	91%
  Antenna 2 Radius \((r_{2})\)	250 mm
  Antenna 2 Efficiency \((η_{2})\)	91%
  \((P_{T})\)	1.2 kW
  Range \((R)\)	120 km
  Frequency \((f)\)	2.7 GHz

• Unknowns: We need to calculate the received power, given the constraints above. We also don’t know the gains for the antennas.

• Assumptions: The communications link relies solely on LOS and not any of the other means (forward scatter, ground wave, or sky wave). Additionally, we can assume the beams of the transmitting antenna and receiving antenna are aligned such that their maximum gains overlap. Lastly, we can assume LOS is established.

Plan: First, we will calculate the wavelength of the signal, then calculate the gain of each antenna, and, finally, use the Friis equation to calculate the received power.

Solve: The wavelength of the transmitted signal is

\[\lambda = \ \frac{c}{f}\ = \ \ \frac{3*10^{8}\ m/s}{2.7*10^{9}\ Hz}\ = 0.1111\ m\ = \ 111.1\ mm\]

We can now calculate the gain of each antenna:

\[G = \ \frac{{(2\pi r)}^{2}}{\lambda^{2}}*\eta\ = \ \frac{{(2\pi*.25\ m)}^{2}}{{(0.1111\ m)}^{2}}*0.91\ = \ \ 181.9\]

Since the gain is the same for both transmitting and receiving, this gain will work for both antennas.

We can now use the Friis equation to calculate the received power.

\[P_{R} = (1.2*10^{3}\ W)(181.9)(181.9)\frac{(0.1111\ m)^{2}}{(4\pi*120,000\ m)^{2}} = 215.5\ nW\ \]

Answer: The receiving antenna receives 215.5 nW of power.

Example Problem 3

A control station uses a monopole antenna on top of a 15’ tower to control an unmanned surveillance aircraft which will be orbiting at an altitude of 3000’ AGL. The station broadcasts an 800 W control signal at a frequency of 300 MHz. The transmitting antenna has a gain of 3.2 and the receiving antenna on the aircraft has a gain of 3.0. If the aircraft needs a minimum of 3.3 nW of power to process the signal, what is the maximum distance the aircraft can be controlled by the ground station?

Understand: The ground control station (GCS) is broadcasting to a UAS in the area and we need to know how far away the UAS can be and still remain under positive control. Note, we are using the minimum required power to solve for the maximum acceptable distance.

Identify Key Information:

• Knowns: We know the following quantities

  Symbol	Value
  P­T­	800 W
  h­UAS­	3000 feet
  h­GCS­	15 feet
  f	300 MHz
  G­T­	3.2
  G­R­	3
  P­R,min­	3.3 nW

• Unknowns: We don’t know the maximum range or the wavelength.

• Assumptions: The communications link relies solely on LOS and not any of the other means (forward scatter, ground wave, or sky wave). Additionally, we can assume the beams of the transmitting antenna and receiving antenna are aligned such that their maximum gains overlap.

Plan: We must solve for both maximum LOS range and the maximum range that the antennas can still communicate with. The second part is a Friis problem, but we need to solve for R, rather than P­_R­.

Solve: First, we calculate the maximum LOS range:

\[r_{max,\ \ total} = \ \sqrt{2h_{station}} + \sqrt{2h_{UAS}}\ = \ \sqrt{2*15} + \ \sqrt{2*3000} = \ 82.94\ miles = 133.5\ km.\]

Now, we rearrange the Friis equation, solving for R:

\[\mathbf{R} = \ \frac{\lambda}{4\pi}\sqrt{\frac{P_{T}G_{T}G_{R}}{P_{R}}}\]

Then, we use the other variables to find our answer. In this case, instead of explicitly solving for the wavelength, we can substitute \(\lambda = \ \frac{c}{f}\ \) to find:

\[\mathbf{R} = \ \ \frac{c}{4\pi f}\sqrt{\frac{P_{T}G_{T}G_{R}}{P_{R}}}\]

Now we can plug in all our numbers and solve for R:

\[\mathbf{R} = \ \ \frac{c\sqrt{P_{T}G_{T}G_{R}}}{4\pi f\sqrt{P_{R}}} = \frac{(3 \times 10^{8}\frac{m}{s})\ \sqrt{800\ W*(3.2)(3.0)}}{(4\pi)(300\ MHz)\sqrt{3.3*\ 10^{- 9}\ W}}\ = \ \ 121.4\ km\]

So, now, w have calculated two ranges: a maximum LOS range of 132.7 km and a maximum power range of 121.4 km. The maximum range the UAS can remain under positive control is the smaller of the two distances, or 121.4 km.

Answer: The maximum distance the aircraft can be controlled is 121.4 km.

Signal-to-Noise Ratio (SNR)

Let’s discuss one final topic for this lesson. Imagine yourself trying to have a conversation with someone in a very noisy room. We can use the signal-to-noise ratio (SNR) to describe how well the other person can hear you:

\[SNR = \frac{signal}{noise} = \ \frac{how\ loud\ you\ are\ talking}{how\ loud\ everyone\ else\ is\ talking}\]

If the other person can understand you, then the SNR is acceptable. If she can’t hear you, the SNR is too low. In this case, you have two options: either increase the signal (talk louder) or decrease the noise (tell everyone else to be quiet). Either option will effectively increase the SNR. In electrical engineering, we describe SNR in terms of power:

\[SNR = \ \frac{P_{signal}}{P_{noise}}\]

In the above example, the noise came from everybody else talking. But, in wireless transmissions, there are several sources of noice: jamming, ambient noise from other signals, and thermal noise. We will discuss jamming in the lesson on Electronic Warfare, and for our purposes, we can assume the ambient noise is small compared to other sources. Thermal noise is caused by the thermal agitation of charge carriers.

Recall that temperature is actually a measurement of the energy of particles in a system. Inside a wireless system, this inherent particle movement manifests as noise, and can interfere destructively as noise. The equation to calculate the power of thermal noise is:

\[P_{noise} = k\left( T_{sys} \right)BW\]

In this equation,

• k is the Boltzmann constant of 1.38 * 10^-23^ J/K.

• T­_sys­ is the effective noise temperature of the system in Kelvin.

• BW is the bandwidth of the signal.

Since we know how to calculate the noise power, the signal-to-noise ratio is therefore:

\[SNR = \ \frac{P_{signal}}{P_{noise}} = \ \frac{P_{R}}{k\left( T_{sys} \right)BW}\]

Example Problem 4

A 500 mm-radius antenna receives 166.0 fW of power. If the received signal has a bandwidth of 10 MHz and the system has an effective temperature of 310 K, what is the signal-to-noise ratio?

Understand: In this situation, we already know how much power arrives at the reciver, but we want to know how the inherent thermal noise of the system affects system performance. In other words, SNR measures how hard we have to work to process the signal.

Identify Key Information:

• Knowns: We know the received power, the radius of the antenna (which is irrelevant, since we already know the received power), the bandwidth of the signal, and the effective temperature of the system.

• Unknowns: Signal-to-noise ratio (SNR).

• Assumptions: Thermal noise is the only appreciable source of noise in the system. Although the effective noise temperature is 310 K, which is equivalent to 98.3° F, this does not mean that the temperature of the antenna is necessarily 98.3°F. Instead, it means that all the energy in the system is equivalent to thermal noise at a temperature of 98.3°F.

Plan: We simply employ the SNR equation to calculate the SNR.

Solve: The SNR equation gives us,

\[SNR = \ \frac{P_{R}}{k\left( T_{sys} \right)BW} = \ \frac{166.0*\ 10^{- 15}W}{\left( 1.38*10^{- 23}\frac{J}{K} \right)(310\ K)(10\ MHz)} = 3.88\]

Answer: For the given system, the signal-to-noise ratio is 3.88, which is very good.

Example Problem 5

You are designing a communication system to receive a signal with a bandwidth of 12 MHz. In order to process the signal, your receiver requires a SNR of 3.5. Assuming the effective noise temperature will not be higher than 320 K, what is the minimum received power required by your system?

Understand: In earlier examples, we knew the minimum received power. Now, however, we need to calculate it.

Identify Key Information:

• Knowns: We know the required SNR, the maximum system temperature, and the bandwidth of the system.

• Unknowns: The minimum received power required to process the signal.

• Assumptions: Thermal noise is the only appreciable source of noise in the system.

Plan: We can rearrange the SNR equation to solve for the received power, P­_R­. Since we know the maximum system temperature and the minimum required SNR, this gives us the worst case scenario, which is the minimum required receive power.

Solve: First, we need to solve the SNR equation for P­_R­:

\[P_{R} = SNR*k\left( T_{sys} \right)BW\]

\[P_{R} = \ 3.5*\left( 1.38*\frac{10^{- 23}J}{K} \right)(320\ K)*12\ MHz = \ 185.5\ fW\]

Answer: The minimum power required by the system is 185.5 fW.

Decibels

While engineering often involves solving complicated mathematical problems, it also often requires representing the results of those problems in graphical form, to make sense of the answers. In electrical engineering, we often deal with units that are several orders of magnitude apart. Consider a radio link, where a radio transmits between 5W and 6W. If we graph the transmit power over time (blue line in Figure 2), it will look like this:

Figure 2: Linear graph of transmit power

The received power on the other end of the communciations link may range between 1μW and 2μW. If we graph the received power on the same graph (red line in following graph), it looks like this:

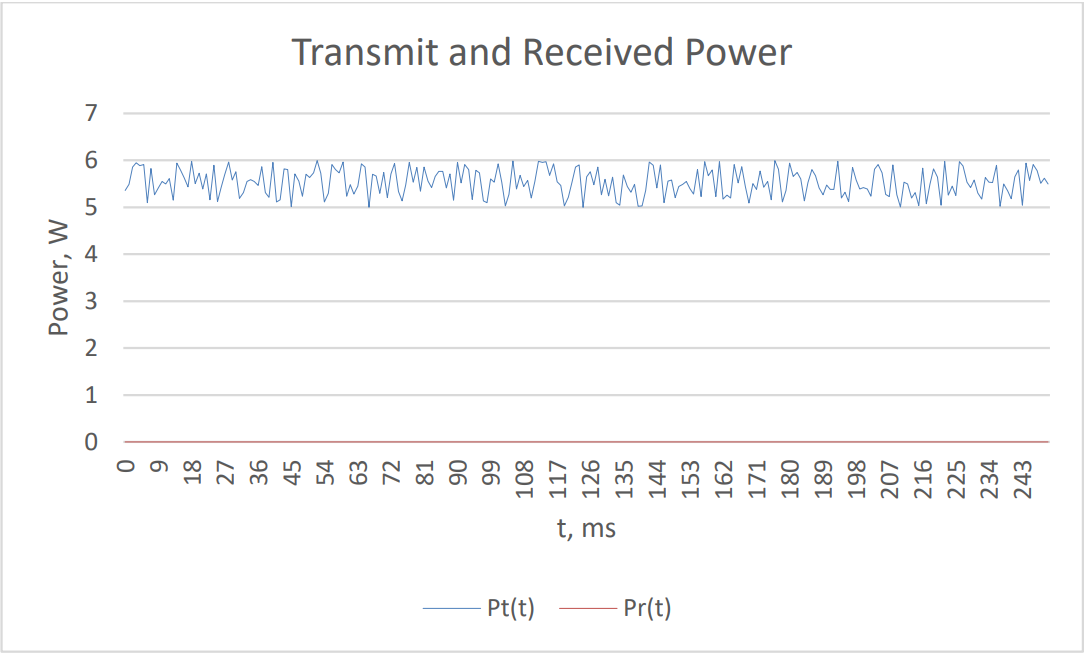
Figure 3: Linear graph of transmit and received power

From this graph, it is impossible to see the variation in the received power. In fact, just by looking at this graph, we might erroneously conclude that no power was received even though the power received is sufficient for communications. If we want to see the variance in received power at the same time as the variance in transmitted power, we need to represent this data in another form.

The solution to this problem in many engineering applications is to change to a logarithmic scale. This value is known as the Decibel. A decibel (dB) is a logarithmic representation of a power ratio[1]. If we have a ratio of powers, which is can be expressed as a gain \(\left( G = \frac{P_{out}}{P_{in}} \right)\), we can convert that ratio to a dB value using the following equation:

\[G_{dB} = 10\ \log_{10}(G)\]

Returning to the radio example above, you might notice that neither the received power nor the transmitted power are ratios. This begs the question of how we can convert such “absolute” quantities to dB. For values that are not ratios, we can still use dB, but we need to establish a reference power. For power, that reference is usually 1W. So, we can represent the transmit power as a dB referenced to a Watt, or a dBW. Sometimes, when dealing with lower powers, we will use 1mW as our reference and the units will be in dBm. To show the applicability, let’s convert the transmitted and received powers above to dBW, which will make the variability in the transmitted and received powers much clearer.

Figure 4: Logarithmic graph of transmit and received power

---

[1]

In other classes, you may see dB used for voltage ratios, and the equation will be slightly different. In order to avoid confusion in this class, we will only use power ratios because this is the strict definition of dB.