Lesson 5 – Circuits 3: Series and Parallel

Learning Outcomes

1. Calculate the current, voltage, power, and equivalent resistance of any circuit with resistors both in series and parallel.

2. Know the voltage and current relationship for resistors in series.

3. Know the voltage and current relationship for resistors in parallel.

4. Be able to apply the voltage and current divider equations to calculate voltages or currents in circuits.

5. Describe the purpose of circuit protection.

6. Determine the required rating of a fuse or circuit breaker to protect a resistive circuit and whether or not a fuse of a certain rating would blow in that circuit.

Series and Parallel Circuits

Last lesson we analyzed circuits containing two different configurations for connecting resistors, or devices that can be modelled as resistors, up to a voltage source. These configurations, known as series and parallel, were deliberately chosen because they represent fundamental ways of connecting devices. The vast majority of circuits we’ll encounter will place its components in either parallel or series (or both) arrangements.

Series Resistors

Looking at the circuit below, we have a “series” arrangement. The resistors are connected end-to-end in a chain. Once those ends are connected to a voltage source, the same amount of current flows sequentially through each device, and each device is subjected to a fraction of the voltage. For a long string of lights, this is a way to apply a small voltage to each light, but a disadvantage is that one bad light will break the circuit, preventing current from flowing.

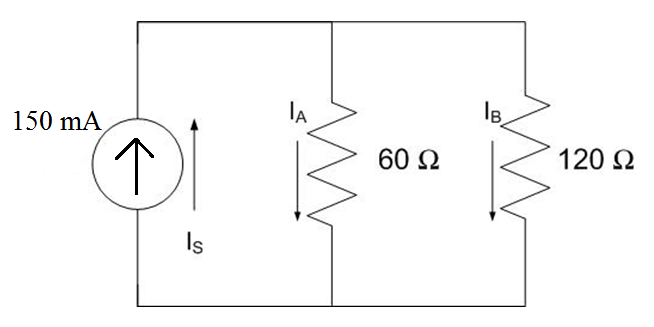
Figure 1: A series circuit with one voltage source and three resistors

Key Concept: When only two components are connected at a node, those components are in series.

Analyzing the series circuit in Figure 1, starting with KVL for the one and only loop, we write:

\[V_{S} - V_{A} - V_{B} - V_{C} = 0\]

\[V_{S} = V_{A}\ {+ \ V}_{B} + V_{C}\]

Each voltage across a resistor can be rewritten using Ohm’s Law:

\[V_{S} = I_{A}R_{A} + I_{B}R_{B} + I_{C}R_{C}\]

Using KCL at each node, we can conclude that our current terms are all equal. A more general conclusion is that any number of resistors in series have the same current.

\[I_{S} = I_{A}{= I}_{B} = I_{C}\]

Key Concept: The current flowing through series components is always the same.

Returning to our KVL equation and substituting all current terms with the term I_S, we have:

\[V_{S} = I_{S}R_{A} + I_{S}R_{B} + I_{S}R_{C}\]

\[{V_{S} = I}_{S}\left( R_{A} + R_{B} + R_{C} \right)\]

\[{V_{S} = I}_{S}R_{EQ(SERIES)}\]

The last step above introduces the term R_EQ(SERIES) where EQ is an abbreviation for “equivalent” and stands in for the sum of all resistances. Moreover, we can replace the three resistors with an equivalent circuit as shown below, allowing us to analyze the circuit’s behavior as if it were just one voltage source and one resistor.

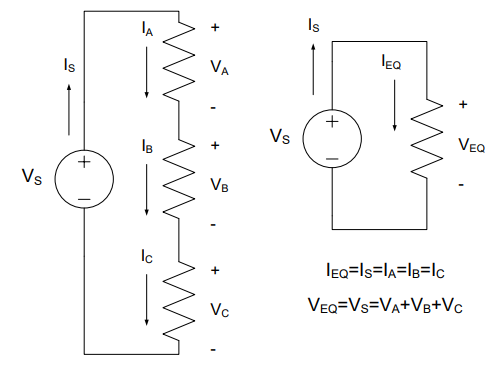
Figure 2: A series circuit and its equivalent

Key Concept: The equivalent resistance of resistors connected in series is the sum of the individual resistances:

\[R_{EQ(SERIES)} = R_{1}{+ R}_{2} + \cdots + R_{n}\]

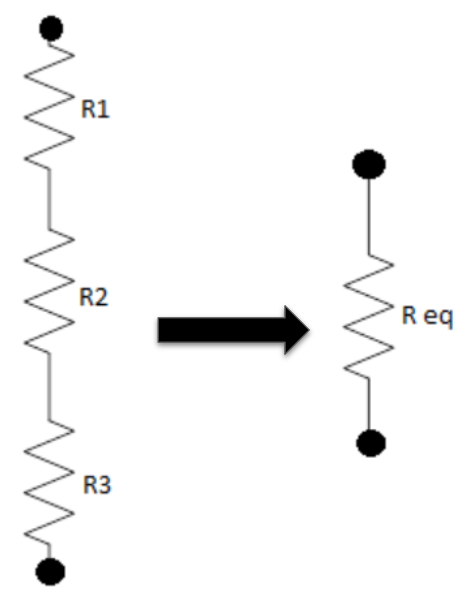
Figure 3: Combining resistors in series into a single resistor

At any location within a circuit, if we find two or more resistors in series, we can simplify them without even knowing the voltage or current. We can sum the resistances and rewrite that portion of the circuit as a single resistor. However, we must be careful that they are actually in series by verifying that there’s nothing else attached to the interior nodes. After all, those interior nodes will “disappear” when the resistors are replaced.

---

Example Problem 1

An inertial navigation system (INS) for a UAS is modeled as 4 resistors in series with a 28-Volt power supply. How much power is being produced by the power supply?

Understand: We have a number of devices (modeled as resistors) connected in series with a voltage source.

Identify Key Information:

• Knowns: resistance values of each component and the source voltage is 28V.

• Unknowns: voltage across each resistor; power produced by the source, P_S.

• Assumptions: all of the power produced by the source is consumed by the load resistors.

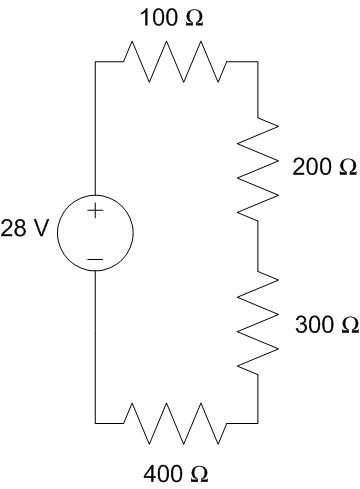
Plan: By consolidating the series resistors into a single equivalent resistor, we can use the power equation to determine the power consumed by the equivalent load. We then assume the source is producing all of the power needed by the load.

Solution: Given V_S = 28V, P_S can be found directly from I_S using a power relationship:

\[P_{S} = I_{S}V_{S}\]

In order to find I_S, we must find a component in the circuit where we know at least two of the four parameters of power, current, voltage, and resistance. For any single resistor, we only know the resistance, but for all the resistors together, the voltage is known.

By simplifying the 4 resistors into single equivalent resistor, there will be a component with enough information to analyze the circuit. Compute equivalent resistance:

\[R_{EQ} = R_{1} + R_{2} + R_{3} + R_{4}\]

\[R_{EQ} = 100\ \Omega + 200\ \Omega + 300\ \Omega + 400\ \Omega = 1\ k\Omega\]

For descriptive purposes, we’ll redraw the circuit using the equivalent resistance and designate this device by the subscript “R_EQ” (referring to the “equivalent resistance”). By KVL, V_REQ = V_S. We can now use the power equation in concert with Ohm’s Law to determine the power consumed by the equivalent resistor.

\[P_{REQ} = \frac{{V_{REQ}}^{2}}{R_{EQ}} = \frac{{(28\ V)}^{2}}{1\ k\Omega} = 784\ mW\]

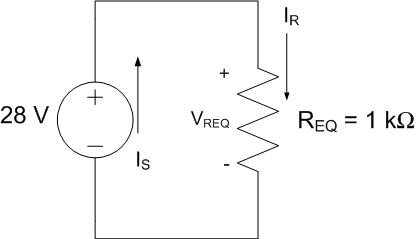
Answer: 784 mW.

---

---

Example Problem 2

Two light bulbs are placed in series in the two circuits below and are each represented by resistors R₁ and R₂. The voltage source in both circuits remains the same, as well as the sum of the resistors. In Circuit #1, the resistors are equal, but for Circuit #2, they are different. For each circuit, how much power is consumed by each light bulb?

Understand: Two light bulbs are connected in series. We want to compare the power consumption as the resistances change between two different circuits.

Identify Key Information:

• Knowns: The resistance values of each bulb and the source voltage, V_S = 9 V.

• Unknowns: Power consumed (P₁ and P₂) for Circuits #1 and #2; current in the circuits

• Assumptions: The bulbs can be modeled as resistors.

Plan: In order to find the power consumed, we must either find the voltage or current through the resistors. Since we don’t have the tools yet to determine the voltages, we can find the current by replacing the two series resistors with a single equivalent resistors. KVL will then give us the voltage across the equivalent resistor.

Solve: The equivalent resistance of each circuit is:

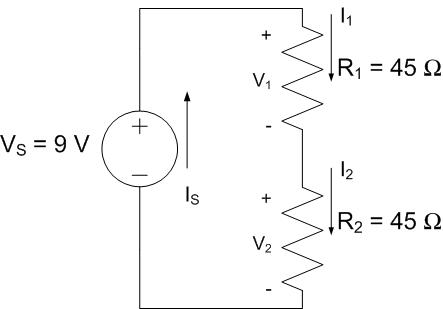
Circuit #1

\[R_{EQ,1} = 45\Omega + 45\Omega = 90\Omega\]

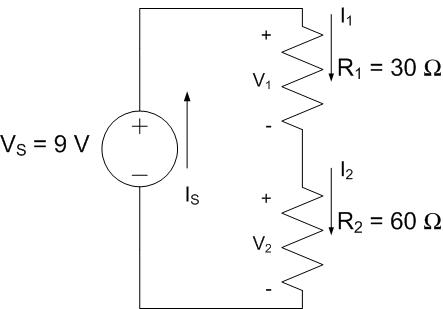
Circuit #2

\[R_{EQ,2} = 30\Omega + 60\Omega = 90\Omega\]

The equivalent resistance for both circuits is the same: 90Ω. This means that we can model both circuits with the circuit below.

By KVL, we see that all 9V is dropped across the 90Ω resistor. Therefore, Ohm’s Law gives the following:

\[9V = \ I_{S}(90\mathrm{\Omega})\ \ \ \ \ thus\ \ \ \ \ I_{S} = \frac{9\ V}{90\ \Omega} = 100\ mA\]

Now, we have all the information we need to calculate the voltages and currents through each resistor in each circuit:

Circuit #1	Circuit #2
\(V_{1} = (45\ \Omega)I_{1}\)	\(V_{1} = (30\ \Omega)I_{1} = (30\ \Omega)(100\ mA) = 3.0\ V\)
\(V_{2} = (45\ \Omega)I_{2} = (45\ \Omega)(100\ mA) = 4.5\ V\)	\(V_{2} = (60\ \Omega)I_{2} = (60\ \Omega)(100\ mA) = 6.0\ V\)
\(P_{1} = I_{1}V_{1} = (4.5\ V)(100mA) = 450\ mW\)	\(P_{1} = I_{1}V_{1} = (3.0\ V)(100\ mA) = 300\ mW\)
\(P_{2} = I_{2}V_{2} = (4.5\ V)(100\ mA) = 450\ mW\)	\(P_{2} = I_{2}V_{2} = (6.0\ V)(100\ mA) = 600\ mW\)

Notice first that the distribution of power and voltage are both proportional to the resistances. Secondly, the sum of the light bulb’s voltage and power values are the same (9V and 900mW) for each circuit and can be checked against the supply’s current and voltage:

\[P_{S} = V_{S}I_{S} = (9\ V)(100\ mA) = 900\ mW\]

Answer: For Circuit #1, \(P_{1} = 450\ mW\) and \(P_{2} = 450\ mW\). For Circuit #2, \(P_{1} = 300\ mW\) and \(P_{2} = 600\ mW\).

---

Voltage Division

For resistors in series, the respective voltages can be calculated using a shortcut known as voltage division. Return to the previous example problem’s circuits depicted below:

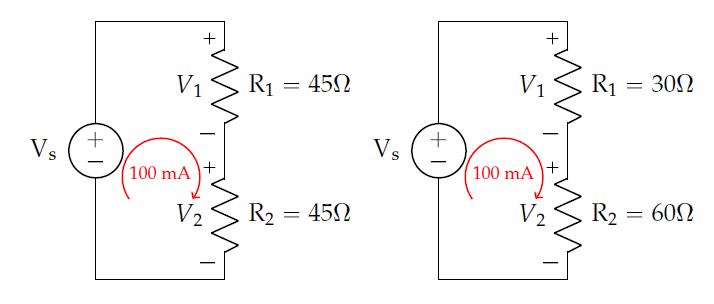
Figure 4: Two series circuits with different resistances but same current

Circuit #1	Circuit #2
\(V_{1} = (45\ \Omega)I_{1} = (45\ \Omega)(100\ mA) = 4.5\ V\)	\(V_{1} = (30\ \Omega)I_{1} = (30\ \Omega)(100\ mA) = 3.0\ V\)
\(V_{2} = (45\ \Omega)I_{2} = (45\ \Omega)(100\ mA) = 4.5\ V\)	\(V_{2} = (60\ \Omega)I_{2} = (60\ \Omega)(100\ mA) = 6.0\ V\)

On the left, the equal resistors drop equal voltages – we just cut 9V in half. One could determine this intuitively without even computing the current. At the right, the results for voltage have the same proportion of the resistor values, a 1:2 ratio. Therefore, we only need to know the relationship between series resistors to analyze voltage.

For a more general case, consider the series resistors in Figure 5 below where I_S is source current, R_EQ is the sum of the three resistances, and the voltage drop across all three is called V_Total:

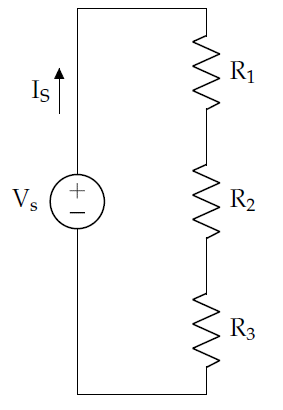
Figure 5: A simple series circuit

\[V_{Total} = I_{S}R_{EQ}\]

\[I_{S} = \frac{V_{Total}}{R_{EQ}}\]

Additionally, for some resistor, X, in this chain (meaning R₁, R₂, or R₃) Ohm’s Law gives:

\[V_{X} = I_{X}R_{X}\]

By KCL, we know that I_X is equal to I_S, so we substitute I_S for I_X and solve for V_X in terms of V_Total and R_EQ:

\[V_{X} = I_{S}R_{X}\]

\[V_{X} = \frac{V_{Total}}{R_{EQ}}*R_{X}\]

Which is typically shown with the resistance of resistor X (\(R_{X}\)) divided by the equivalent resistance (\(R_{EQ}\)) to highlight the fact that voltage drop is proportional to the ratio of the resistances. This equation, commonly known as the voltage divider, is shown below.

\[V_{X} = \frac{R_{X}}{R_{EQ}}V_{Total}\]

The voltage divider only works for resistors in series and is often simpler to employ than a complete implementation of KVL and KCL.

Key Concept: The voltage divider equation determines how voltage is proportionally divided between any number of series resistors.

---

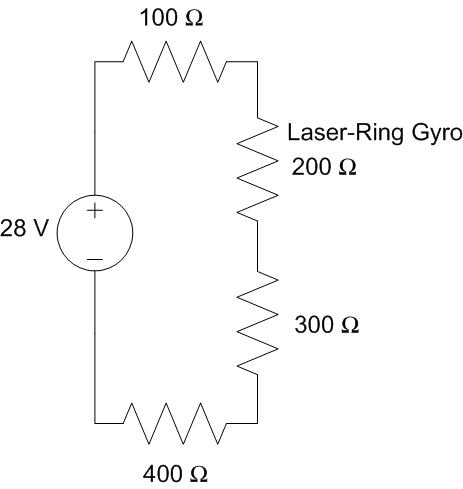
Example Problem 3

An inertial navigation system (INS) for a UAS is modeled as 4 resistors in series with a 28-Volt power supply. What is the voltage drop across the laser-ring gyro, which is modeled as a 200-Ω resistor?

Understand: We have several resistors in series with a voltage source. We want to know the voltage across one of the resistors in the middle of the circuit.

Identify Key Information:

• Knowns: V_S, the resistance values

• Unknowns: V_200Ω

• Assumptions: None.

Plan: We can use the voltage divider to get right to the voltage value of the laser-ring gyro.

Solve: Applying the voltage divider equation with R_X = 200 Ω, we get:

\[V_{X} = \frac{200\ \Omega}{100\ \Omega + 200\ \Omega + 300\ \Omega + 400\ \Omega}(28\ V)\]

\[V_{X} = \frac{200\ \Omega}{1k\Omega}(28\ V) = 5.6\ V\]

Answer: The voltage drop across the laser-ring gyro is 5.6 V.

---

---

Example Problem 4

You have two 150-Ω resistors and a third resistor of unknown value, all in series and subjected to a 6V source. If 1 V is desired across this third unknown resistor (R_A), what should the value of R_A be?

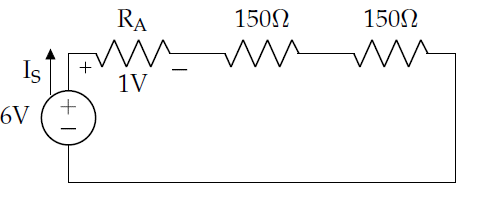
Understand: We have three resistors in series, and need to find the resistance that will make the circuit “work” as desired (that is, the unknown resistor will drop 1V).

Identify Key Information:

• Knowns: VS = 6 V, the other resistance values, VA = 1 V

• Unknowns: Ra, Is

• Assumptions: None.

Plan: Ultimately, we want to use the voltage divider to determine the voltage proportionality between R_A and the other resistors. First, though, we can combine the two 150 Ω resistors to an equivalent 300 Ω resistor. Then, we can use the voltage divider equation to determine the total equivalent resistance of the circuit. Finally, since resistors in series add, we can subtract off the 300 Ω resistor to determine the unknown resistance.

Solve: Given that the source is 6V and the voltage across R_A is 1V, we can use KVL to determine the remaining voltage drop (across the equivalent 300 Ω resistor) is 5V. Now we’re ready to use a voltage divider equation, and then we’ll rearrange it to solve for R_EQ.

\[V_{X} = \frac{R_{X}}{R_{EQ}}V_{Total}\]

\[R_{EQ} = \frac{R_{X}}{V_{X}}V_{Total}\]

Set R_X to 300 Ω, V_X to 5V, and V_Total to 6V.

\[R_{EQ} = \frac{300\mathrm{\Omega}}{5V}6V = 360\mathrm{\Omega}\]

Finally, since R_EQ =300Ω + R_A = 360Ω, we can conclude R_A = 60Ω.

Answer: A 60-Ω resistor will provide the needed 1V.

---

Parallel Resistors

The other basic arrangement of devices is to place them in parallel. Instead of the devices being connected end-to-end, each device shares the same two nodes. Figure 6 below shows three resistors and a voltage source connected in parallel.

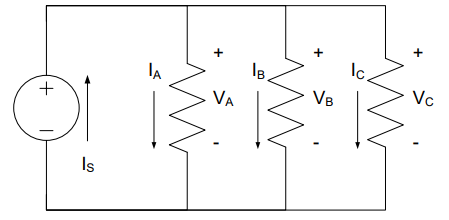
Figure 6: A parallel circuit with one voltage source and three resistors

When we apply KVL to this circuit, we find that all the voltage drops across all the resistors are the same:

\[V_{S} = V_{A}{= V}_{B} = V_{C}\]

This identity is the foundation of parallel equivalent resistance.

Key Concept: Devices in parallel have the same voltage drop across them.

Inspecting either node with KCL, we find that:

\[\ I_{S} = I_{A}\ {+ \ I}_{B} + I_{C}\]

Substituting the current through each resistor using Ohm’s Law, we have:

\[I_{S} = \frac{V_{A}}{R_{A}} + \frac{V_{B}}{R_{B}} + \frac{V_{C}}{R_{C}}\]

Since the voltages V_A = V_B = V_C = V_S, this equation simplifies to:

\[I_{S} = \frac{V_{S}}{R_{A}} + \frac{V_{S}}{R_{B}} + \frac{V_{S}}{R_{C}} = V_{S}\left( \frac{1}{R_{A}} + \frac{1}{R_{B}} + \frac{1}{R_{C}} \right)\]

And rearranges to:

\[V_{S} = \frac{1}{\frac{1}{R_{A}} + \frac{1}{R_{B}} + \frac{1}{R_{C}}}I_{S} = R_{EQ(PARALLEL)}I_{S}\]

Where we have introduced R_EQ(PARALLEL) as the reciprocal of the sum of the reciprocals of individual resistances. Much as we did with resistors in series, we can replace the three resistors in Circuit #1 with an “equivalent” circuit as shown on the next page, giving us a much simpler circuit to analyze.

Key Concept: The equivalent resistance for resistors in parallel is given by

\[R_{EQ(PARALLEL)} = \frac{1}{\frac{1}{R_{1}} + \frac{1}{R_{2}} + \ldots + \frac{1}{R_{n}}}\]

We are not limited to only having three resistors in parallel; as the parallel equivalent resistance equation above shows, we can have two or more resistors placed in parallel.

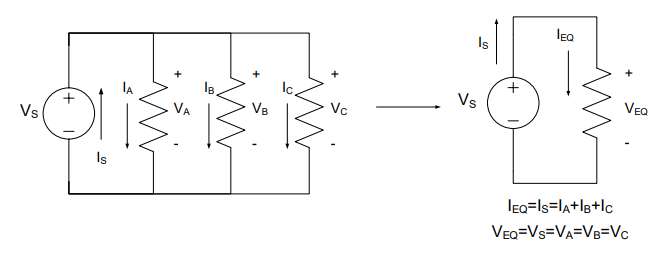
Figure 7: A parallel circuit and its equivalent

For parallel resistors, if we specialize the equivalent resistance equation to only two resistors (here, R_X and R_Y), we find the following equation:

\[R_{EQ(PARALLEL)} = \frac{1}{\frac{1}{R_{X}} + \frac{1}{R_{Y}}} = \frac{1}{\frac{R_{Y}}{R_{Y}R_{X}} + \frac{R_{X}}{R_{X}R_{Y}}} = \frac{1}{\frac{R_{Y} + R_{X}}{R_{X}R_{Y}}} = \frac{R_{X}R_{Y}}{R_{X} + R_{Y}}\]

This equation is a convenient shortcut when only two resistors are in parallel. This shortcut does not extend to three or more resistors in parallel, and in such cases, the equivalent resistance equation at the top of this page must be used.

---

Example Problem 5

A cooling fan, which is modeled as a 30-Ω resistor, is powered by a 2.4-V battery. To monitor the battery, a voltmeter with a resistance of 660 kΩ is added in parallel as shown. How much resistance does the voltage source now see?

Understand: For any circuit, the amount of resistance the voltage source “sees” is the equivalent resistance of the circuit. Therefore, we are trying to simplify a circuit with two parallel resistors connected to a 2.4V source. Since the resistance of the meter is significantly larger than that of the fan, we expect the fan to consume most of the current. We know this is true for two reasons: parallel resistors share the same voltage and Ohm’s Law tells us that, for the same voltage, a lower resistance will have a higher current. From KCL, we know that the currents through the fan and the meter will add at the top and bottom nodes to become the source current. If we were to divide the source voltage by the source current, we would get a resistance, and this resistance would be the equivalent resistance of the circuit. Since the fan is the primary contributor to the source current, it has the largest impact on the equivalent resistance. Therefore, the resistance of the fan will be most of what the source “sees”.

Identify Key Information:

• Knowns: V_S = 2.4 V, R_fan = 30Ω, R_meter= 660kΩ

• Unknowns: R_EQ

• Assumptions: None

Plan: We will use the equation for finding equivalent resistance of resistors in parallel. We can either use the generic equation or the specialized equation for only two resistors.

Solve: Using the specialized equation for two resistors in parallel, we have:

\[R_{EQ(PARALLEL)} = \frac{(660\ k\Omega)(30\ \Omega)}{(660\ k\Omega) + (30\ \Omega)} = 29.9986\ \Omega = 30\Omega\]

Answer: The equivalent resistance of the circuit is 30 Ω.

As stated in the “Understand” section of this example, we could use the source voltage and current to solve for the equivalent resistance of the circuit. We will prove that here.

\[I_{S} = I_{fan} + I_{meter} = \frac{2.4\ V}{30\ \Omega} + \frac{2.4\ V}{660\ k\Omega} = 80\ mA + 3.64\ \mu A = 80.004\ mA\ \]

\[R_{EQ(PARALLEL)} = \frac{V_{S}}{I_{S}} = \frac{2.4\ V}{80.004\ mA} = 29.9985\ \Omega = 30\ \Omega\]

The equivalent resistance of a circuit is the ratio of the source voltage to the source current; for that reason, we say that the equivalent resistance of a circuit is what the source “sees”.

Note: Because the voltmeters’s resistance is 22,000 times higher than the cooling fan’s resistance, the equivalent resistance is effectively the same as if there was no voltmeter in the circuit. An important feature of a voltmeter and other monitoring equipment is that they don’t interfere with circuits by modifying their behavior when attached to a circuit.

---

---

Example Problem 6

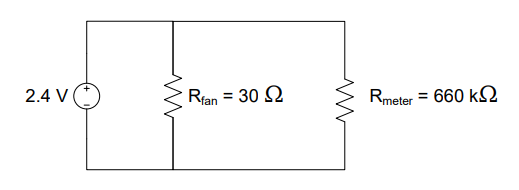
A voltage source that supplies 6 V is used to charge various cell phones connected in parallel. Two different types of phones are currently being charged, one modeled as a 120-Ω resistor and the other as a 60-Ω resistor. How much power does the voltage source provide?

Understand: We have a circuit with a 6-V source connected to two resistors in parallel.

Identify Key Information

• Knowns: V_S = 6 V, R_A = 60 Ω, R_B= 120 Ω

• Unknowns: Power, P_S, provided by the voltage source; currents I_S, I_A, and I_B

• Assumptions: The source provides all the power needed by the load.

Plan: We eventually want to use the power equation to determine how much power the source is providing. Since we know the voltage of the source and the resistances, we can use the power equation in conjuntion with Ohm’s Law (\(P = \ \frac{V^{2}}{R}\)). However, we need to ensure we use the equivalent resistance for the parallel resistors (\(R_{EQ} = \ \frac{R_{1}R_{2}}{R_{1} + R_{2}}).\ \)

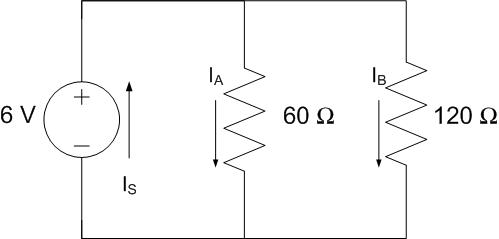
Solve: Using equivalent resistance, this circuit can be simplified as shown below, replacing resistors R_A and R_B with R_EQ:

Where R_EQ is given by the equivalent resistance formula for parallel resistors:

\[R_{EQ} = \frac{(60\ \Omega)(120\ \Omega)}{60\ \Omega + 120\ \Omega} = 40\ \Omega\]

Notice that the equivalent resistance is smaller than the smallest resistor value.

Next, we can solve for the power provided using Ohm’s Law and the Power Equation:

\[P_{S} = \frac{{V_{S}}^{2}}{R_{EQ}} = \frac{{(6V)}^{2}}{40\Omega} = \ 900\ mW\]

Answer: The power provided by the source is 900 mW.

Note: There are other solution methods. The fact that the resistors are in parallel tells us that:

\[6\ V = V_{A} = V_{B}\]

and since the sum of power consumed is equal to power provided:

\[P_{S} = P_{A} + P_{B} = \frac{(6\ V)^{2}}{60\ \Omega} + \frac{(6\ V)^{2}}{120\ \Omega} = 600\ mW + 300\ mW = 900\ mW\]

---

Current Division

For resistors in parallel, we can develop a KCL-based shortcut similar to the voltage divider introduced earlier in this reading. Consider the circuit below:

Figure 8: A parallel circuit with two resistors and a voltage source

From KVL, we already know that each resistor has a 6-V drop. Using Ohm’s Law, we can determine which resistor has more current flowing through it:

\[I_{A} = \frac{V_{A}}{60\ \Omega} = \frac{6\ V}{60\ \Omega} = 100\ mA\]

\[I_{B} = \frac{V_{B}}{120\ \Omega} = \frac{6V}{120\ \Omega} = 50\ mA\]

No doubt you have heard something similar to the following statement: Electricity prefers the path of least resistance. We can see in the circuit above that this is true. More current flows through the smaller 60-Ω resistor than through the larger 120-Ω resistor. In fact, twice as much current flows through the 60-Ω resistor because it is half the size of the 120-Ω resistor. In general, for parallel resistors R_X, R_Y, and R_Z with equivalent resistance R_EQ, the voltage across resistor R_X, V_X, is equal to the voltage across R_EQ, V_Total. This is true because the voltages across the parallel resistors are equal:

\[V_{X} = V_{Total}\]

\[I_{X}R_{X} = \ I_{Total}R_{EQ}\]

Rearranging to find I_X, we have the general current divider equation:

\[I_{X} = \frac{R_{EQ}}{R_{X}}I_{Total}\]

The current divider equation only works for resistors in parallel and may be quicker than using KVL, KCL, and Ohm’s Law to solve for currents.

Key Concept: The current divider equation determines how current is proportionally divided between any number of parallel resistors.

Now, if there are only two resistors, R_EQ can be written in terms of R_X and R_Y giving us the two-resistor current divider equation:

\[I_{X} = \left( \frac{R_{X}R_{Y}}{R_{X} + R_{Y}} \right)\frac{1}{R_{X}}I_{Total} = \frac{R_{Y}}{R_{X} + R_{Y}}I_{Total}\]

The two-resistor current divider equation skips finding equivalent resistance. With three or more resistors, we must find R_EQ and use the general current divider.

---

Example Problem 7

In the circuit represented below, how much current passes through the 120-Ω resistor (I_B)?

Understand: Instead of the typical voltage source, here we have a current source. In this case, the source provides a constant current of 150 mA. We have two resistors in parallel and want to find the current through one of them.

Identify Key Information:

• Knowns: I_S = 150mA, R_A = 60Ω, R_B= 120Ω

• Unknowns: currents I_A, and I_B

• Assumptions: None.

Plan: We can use a straightforward current divider (for two resistors only) to find the desired current.

Solution: We can use two-resistor current division to find the current, being careful to properly assign the values. The two resistor current divider formula is:

\[I_{Y} = \frac{R_{X}}{R_{X} + R_{Y}}I_{Total}\]

Which, in this case, is:

\[I_{B} = \frac{R_{A}}{R_{A} + R_{B}}I_{Total}\]

\[I_{B} = \frac{60\ \Omega}{60\ \Omega + 120\ \Omega}(150\ mA) = 50\ mA\]

Answer: The current passing through the 120-Ω resistor is 50 mA.

Additionally, there is 100 mA of current passing through the 60-Ω resistor. Thus, where the resistors in parallel have a 1:2 ratio of resistance, their currents have a 2:1 ratio.

---

Voltage Adapters

Oftentimes, in real life, we cannot control the source voltage, and our load may require a lower voltage. What do we do with the “extra” voltage (KVL tells us it has to go somewhere)? We can use what is called a voltage adapter. The adapter’s job is to “soak up” some of the voltage in the circuit, thereby reducing the voltage across a particular load to meet design criteria. Now, it may show up in our circuits as a generic box as opposed to the traditional zig-zag resistor, such as in the circuit below. We draw a box for convenience; since we haven’t specified the arrangement or the number of resistors to place inside, it’s easier to represent the adapter as a “black box”.

Example Problem 8

Determine the resistance required for a voltage adapter so that it can allow a 12-V lamp (modeled as a 2-kΩ load) to be used with an 18-V source. The voltage adapter is placed in series with the lamp, as shown below.

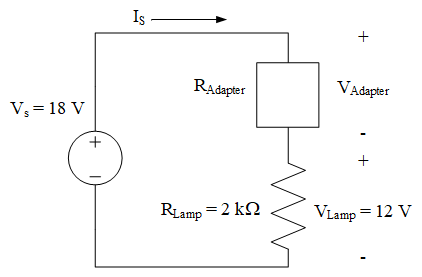
Understand: Here, we have a lamp that has a maximum voltage rating of 12V. We need a voltage adapter to “soak up” the extra voltage from the voltage source. The question is asking us to find the resistance of the voltage adapter.

Identify Key Information:

• Knowns: V_S = 18V, R_Lamp = 2kΩ, V_Lamp = 12V

• Unknowns: R_Adapter and V_Adapter

• Assumptions: None.

Plan: In order to find the resistance of the adapter, we will need to use Ohm’s Law. In order to use Ohm’s Law, we will need to know the current through and voltage across the adapter. We can use Ohm’s Law to find the current in the series circuit since we have the voltage and resistance of the lamp. We can find the voltage across the adapter via KVL. So, we will find I_S by Ohm’s Law, then V_Adapter via KVL, and then use that voltage to find R_adapter.

Solve: By using Ohm’s Law with the lamp voltage and resistance, we can find the current through the lamp:

\[I_{Lamp} = \ \frac{12V}{2k\Omega} = 6\ mA\]

Since we have a series circuit, the same current must flow through the entire circuit, so \(I_{S}\) and \(I_{Adapter}\) must be equal to 6 mA as well.

Secondly, applying KVL to this circuit gives us one equation. We can use this equation to solve for V_Adapter.

\[18\ V - V_{Adapter} - V_{Lamp} = 0\]

\[V_{Adapter} = 18\ V - V_{Lamp} = 18\ V - 12\ V = 6\ V\]

Finally, we can use Ohm’s Law to find the resistance R_Adapter:

\[R_{Adapter} = \ \frac{V_{Adapter}}{I_{Adapter}} = \ \frac{6\ V}{6\ mA} = 1\ k\mathrm{\Omega}\]

Answer: A 1-kΩ resistor in series can serve as the voltage adapter.

If only 2-kΩ resistors were available, how could this be done? Placing two 2-kΩ resistors in parallel would provide a 1-kΩ voltage adapter.

---

Fuses and Breakers

Bad things can happen if we fail to keep electricity under control: equipment can be damaged; buildings can catch fire; and people can be injured, or even killed. Fortunately, using simple devices like fuses and circuit breakers can protect us and our circuits if something goes wrong. When selecting fuses and circuit breakers for our circuits, we must use sound engineering analysis because selecting the wrong fuse or circuit breaker could prevent the circuit from working or be ineffective in protecting the circuit. The outcome will be dependent upon whether the rating of the fuse or circuit breaker was too high or too low for the circuit.

Many of you have probably heard of the term, “short circuit,” and know that it’s “bad” (in the smoke pouring out of your electrical device kind of “bad”). A short circuit is simply a wire that connects the positive terminal of a voltage source directly to the negative terminal as in the example circuit below.

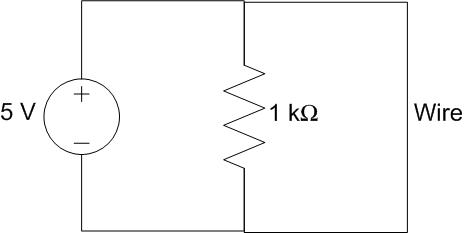
Figure 9: A circuit containing a short circuit

So in this scenario, how much current will be drawn from the source? Well, we’ve learned today that solving for a circuit’s equivalent resistance allows us to model the circuit as a source and a single resistor. So what is the equivalent resistance of the circuit above? If we model the wire as a 0-Ω resistor, we can solve for the equivalent resistance of the circuit (you saw that they were in parallel already, right?):

\[R_{EQ(PARALLEL)} = \frac{(1\ k\Omega)(0\ \Omega)}{(1\ k\Omega) + (0\ \Omega)} = 0\ \Omega\]

What this means is that the voltage source only “sees” the wire, which we modelled as a 0-Ω resistor. Because of this, all of the current will flow through the short circuit, leaving none to flow through the resistor. Therefore, the circuit can be redrawn as:

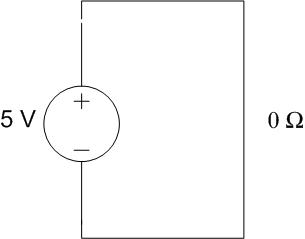
Figure 10: An equivalent circuit for a circuit containing a short circuit

Since the wire and the source are parallel, we know 5 V has to drop across the wire. Using Ohm’s Law to solve for current,

\[I_{S} = \frac{V_{S}}{R_{EQ}} = \frac{6\ V}{0\ \Omega} = \infty\ A\]

In reality, the current is not infinite. The wire itself has a small amount of resistance, which will keep the current from going to infinity.

The important point, though, is that a short circuit causes a very large amount of current to be drawn from the source. In the wiring in a house, for example, a short circuit can draw enough current to melt a wire’s plastic coating and cause any wood or insulation near the wire to catch fire. This, obviously, is a bad thing. In addition to fires, short circuits can melt wires and destroy electrical components. To prevent this from occurring, engineers incorporate fuses and circuit breakers into their designs.

A fuse is nothing more than a very thin wire which usually allows the current of a circuit to flow. Under normal conditions, the current flow is low enough for the fuse to act as a simple wire. As the current increases, however, the wire begins to heat until at some point, the fuse melts, severing the connection and stopping the flow of current.

The highest current a fuse can handle without melting is the rating of the fuse. A fuse rated at 2 amps will be able to handle anything up to 2 amps. Once the current rises above 2 amps, it will melt.

Figure 11: A good fuse and blown fuses (Source: Electronicrepairguide.com)

A circuit breaker (or breaker) has the exact same function as a fuse but has an advantage over the fuse in that it doesn’t have to be replaced every time it “blows.” Most modern house and aircraft wiring systems have circuit breakers while most cars still have fuses. Like the fuse, the circuit breaker protects against current surges and has its rated capability printed on it. Circuit breakers are a more expensive investment at first but, usually, pay for themselves over a lifetime. Breakers generally consist of a spring-loaded switch that is held closed by a catch. The catch is released when the current level gets too high, opening the circuit to prevent damage. Usually, the breaker is reset by flipping a lever or pushing a button.

So what rating do we choose for our fuse or circuit breaker? There are two rules to consider when choosing ratings:

1. The rating must be higher than the expected current in the circuit.

2. The rating must be lower than the failure point of the wiring.

For ECE 315, we will calculate fuse or circuit breaker ratings in a very specific way. First, we will calculate the maximum current that could be flowing through the fuse or circuit breaker under normal operating conditions. Next, we will multiply this current by 1.1 (adding 10% to the current), and then we will round that up to the nearest whole or half number within the units dictated by proper engineering notation. This means that if, after multiplying by 1.1, the current is in milliamps, round up to the nearest milliamp, but if the current is in amps, round up to the nearest amp.

---

Example Problem 9

The internal circuitry of a battery powered camera is modeled as the resistive circuit below. What fuse rating would you choose to protect the circuit?

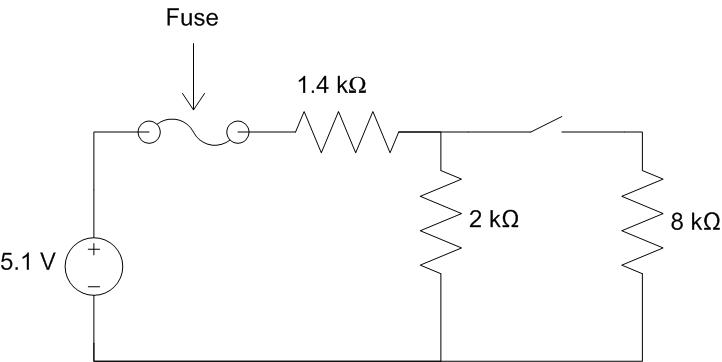
Understand: In order to determine the fuse rating, we must find the current drawn from the source. We’ve added a switch which allows current to flow through to the 8-kΩ resistor when it’s closed and blocks the current when it’s open. And the circuit includes both series and parallel conncections. The circuit’s equivalent resistance (and thus the source current drawn from the voltage source) will change based on whether the switch is open or closed.

Identify Key Information:

• Knowns: We know the values of the voltage source and the resistors

• Unknowns: The total current drawn from the source by the load and the fuse rating.

• Assumptions: The resistance in the wire is much smaller than that of the resistors.

Plan: We will determine the current drawn from the source when the switch is both open and closed. The fuse rating can be determined once we see which configuration draws more current.

Solve: When the switch is open, no current gets to the 8-kΩ resistor and therefore it has no effect on the circuit. If we model the fuse as a wire (since we will assume it is not blown) and remove all hanging wires/components, the circuit simplifies to the circuit below: a 5.1-V source in series with the 1.4-kΩ and the 2-kΩ resistors.

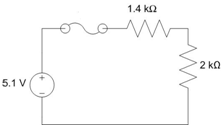
Solving for the equivalent resistance gives us:

\[R_{EQ} = 1.4\ k\Omega + 2\ k\Omega = 3.4\ k\Omega\]

Redrawing the circuit leads to:

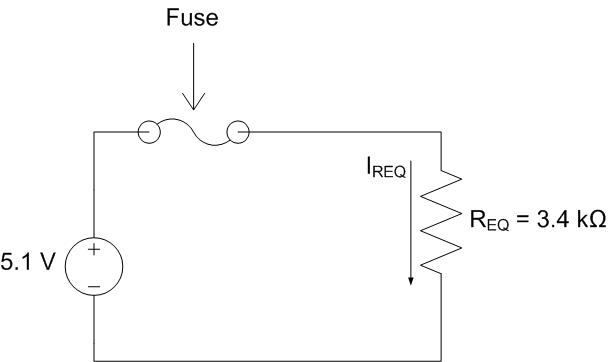
Since we model the fuse as a wire, R_EQ drops all 5.1 volts. The current through R_EQ is therefore:

\[I_{EQ} = \frac{V_{S}}{R_{EQ}} = \frac{5.1\ V}{3.4\ k\Omega} = 1.5\ mA\]

Since R_EQ is in series with the source and the fuse, all three devices share the same current. Therefore the fuse rating has to be greater than 1.5 mA.

Now, we will repeat the analysis with the switch closed. Note the switch is also modeled as a wire when it’s closed.

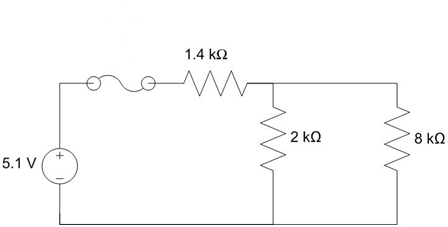
The 2 kΩ and 8 kΩ resistors are parallel, so we can combine them with the equation:

\[R_{EQ(PARALLEL)} = \frac{(2\ k\Omega)(8\ k\Omega)}{(2\ k\Omega) + (8\ k\Omega)} = 1.6\ k\Omega\]

We can now redraw the circuit using this value:

We can now find the equivalent resistance for the entire circuit:

\[R_{EQ} = 1.4\ k\Omega + R_{EQ(PARALLEL)} = 1.4\ k\Omega + 1.6\ k\Omega = 3\ k\Omega\]

Redrawing the circuit leads to:

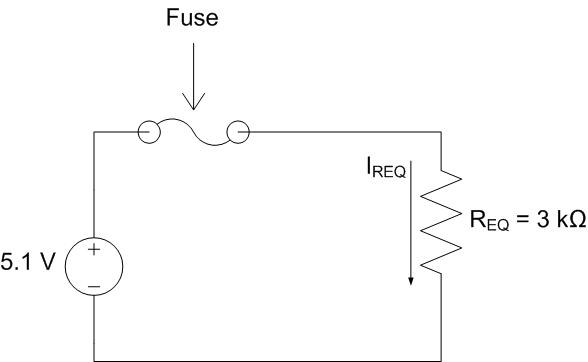
Again, R_EQ drops all 5.1 volts. The current through R_EQ is

\[I_{EQ} = \frac{V_{S}}{R_{EQ}} = \frac{5.1\ V}{3\ k\Omega} = 1.7\ mA\]

With the switch closed, the current through the fuse is 1.7 mA. With the switch open, the current through the fuse is only 1.5 mA. Since we want the circuit to work whether the switch is open or closed, we need the fuse to be rated higher than the highest current, 1.7 mA.

Since the maximum current through the fuse under normal operating conditions is 1.7 mA, we multiplying this by 1.1 to get 1.87 mA. Rounding 1.87 mA up to the nearest whole or half number (also the nearest milliamp for this problem) gives us a fuse rating of 2 mA.

Answer: We would choose a fuse with a 2 mA rating to protect this circuit.

---