Practice Problems (KEY)

Practice Problems (KEY)#


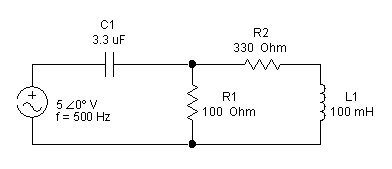
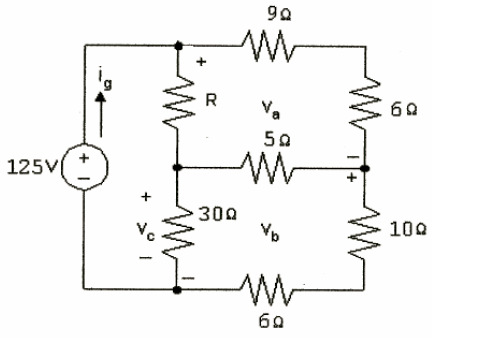
How many nodes and how many loops are in each of the circuits below?

  • Nodes: 4 Nodes: 6

  • Loops: 3 Loops: 7


  • Nodes: 4 Nodes: 4

  • Loops: 1 Loops: 7

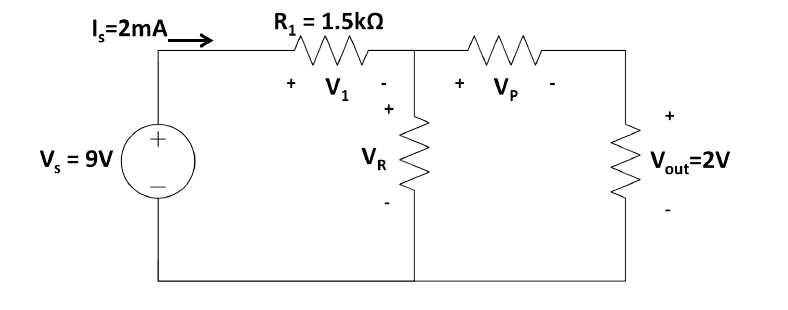
Find \(V_R\) and \(V_P\).

\[ V_1 = (2\,\mathrm{mA})(1.5\,\mathrm{k}\Omega) = 3\,\mathrm{V} \]
\[ V_S - V_1 - V_R = 0 \]
\[ V_R = V_S - V_1 = 9\,\mathrm{V} - 3\,\mathrm{V} = 6\,\mathrm{V} \]
\[ V_R - V_P - V_{\mathrm{out}} = 0 \]
\[ V_P = V_R - V_{\mathrm{out}} = 6\,\mathrm{V} - 2\,\mathrm{V} = 4\,\mathrm{V} \]

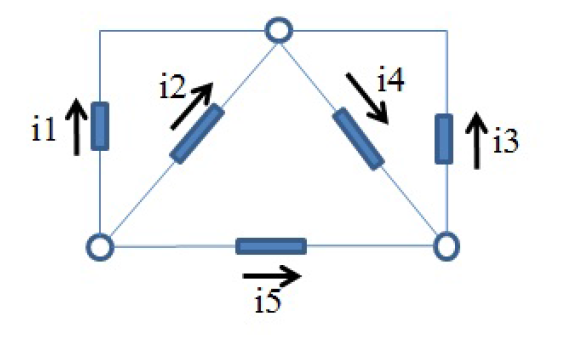
If \(i_2=-2\,\mathrm{A}\), \(i_3=-5\,\mathrm{A}\), and \(i_4=4\,\mathrm{A}\), find \(i_1\) and \(i_5\).

\[ i_5 + i_4 - i_3 = 0 \]
\[ i_5 = -i_4 + i_3 = -(4\,\mathrm{A}) + (-5\,\mathrm{A}) = -9\,\mathrm{A} \]
\[ i_1 + i_2 + i_3 - i_4 = 0 \]
\[ i_1 = -i_2 - i_3 + i_4 = -(-2\,\mathrm{A}) - (-5\,\mathrm{A}) + 4\,\mathrm{A} = 11\,\mathrm{A} \]

  1. Answer the following questions about the circuit below.

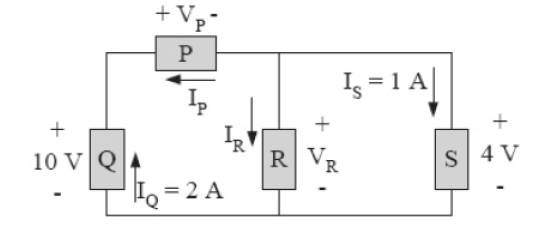
a. How many nodes and loops are in this circuit?

  • Nodes: 3

  • Loops: 3

b. Write out the KVL and KCL equations for the circuit.

  • \(V_Q - V_P - V_R = 0\)

  • \(V_R - V_S = 0\)

  • \(V_Q - V_P - V_S = 0\)

  • \(I_Q + I_P = 0\)

  • \(-I_P - I_R - I_S = 0\)

  • \(-I_Q + I_R + I_S = 0\)

c. Solve for the power consumed by each component in this circuit.

  • \(V_S=4\,\mathrm{V}\), \(V_R=4\,\mathrm{V}\), \(V_P=6\,\mathrm{V}\), \(V_Q=10\,\mathrm{V}\)

  • \(I_S=1\,\mathrm{A}\), \(I_R=1\,\mathrm{A}\), \(I_P=-2\,\mathrm{A}\), \(I_Q=2\,\mathrm{A}\)

  • \(P_S=4\,\mathrm{W}\), \(P_R=4\,\mathrm{W}\), \(P_P=12\,\mathrm{W}\), \(P_Q=20\,\mathrm{W}\)

  1. Use KVL and KCL to solve for the unknown voltages and currents in the circuits below.

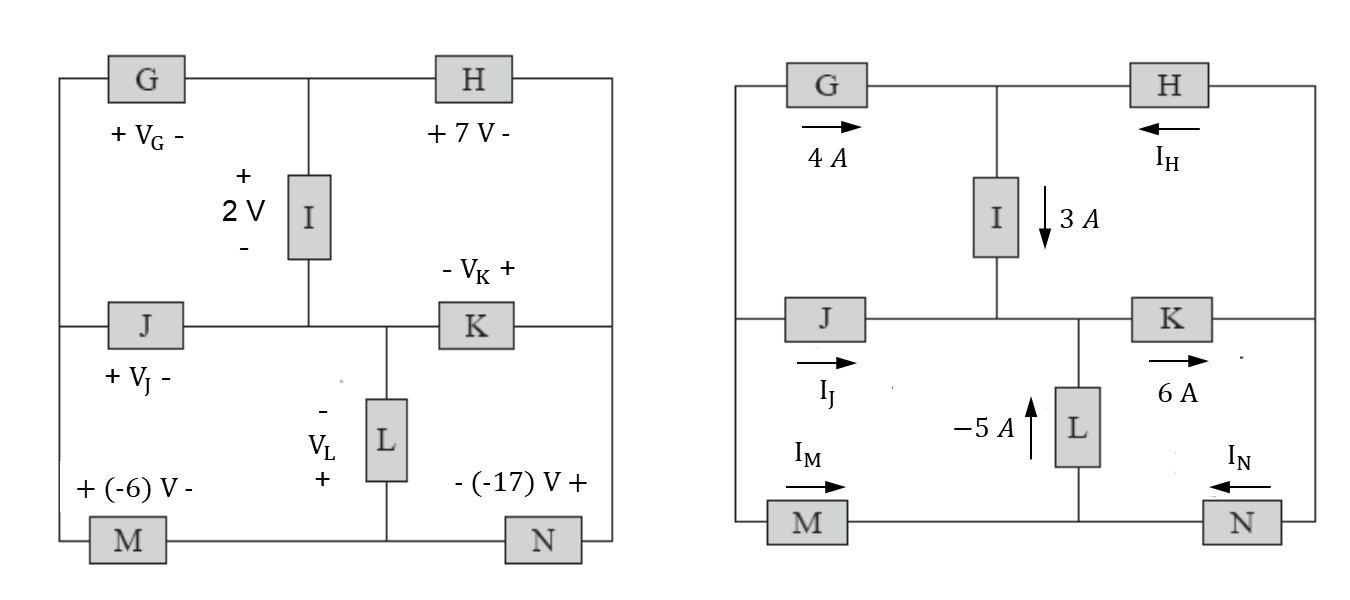
KVL Equations

KCL Equations

\(-V_G - 2\,\mathrm{V} + V_J = 0\)

\(4\,\mathrm{A} + I_H - 3\,\mathrm{A} = 0\)

\(2\,\mathrm{V} - 7\,\mathrm{V} - V_K = 0\)

\(3\,\mathrm{A} + I_J - 5\,\mathrm{A} - 6\,\mathrm{A} = 0\)

\(-V_L + V_K + 17\,\mathrm{V} = 0\)

\(I_M + I_N + 5\,\mathrm{A} = 0\)

\(-V_J + V_L - 6\,\mathrm{V} = 0\)

\(6\,\mathrm{A} - I_N - I_H = 0\)

\(V_G = 4\,\mathrm{V}\)

\(I_M = -I_N - 5\,\mathrm{A}\)

  1. A satellite control module is connected to a data processing element modeled as a single \(12.5\,\mathrm{k}\Omega\) resistor (\(R_2\)). The system is powered by a \(5\,\mathrm{V}\) solar cell (\(V_S\)). Control module options are modeled as resistors with values:

  • \(R_1 = 5\,\mathrm{k}\Omega\)

  • \(R_1 = 10\,\mathrm{k}\Omega\)

  • \(R_1 = 15\,\mathrm{k}\Omega\)

  1. If the circuit in the previous problem has the following requirements, which of the three options are viable?

  • Total current must not exceed \(250\,\mu\mathrm{A}\)

  • Voltage across the control module (\(V_1\)) must be at least \(2\,\mathrm{V}\)