Practice Problems (KEY)#
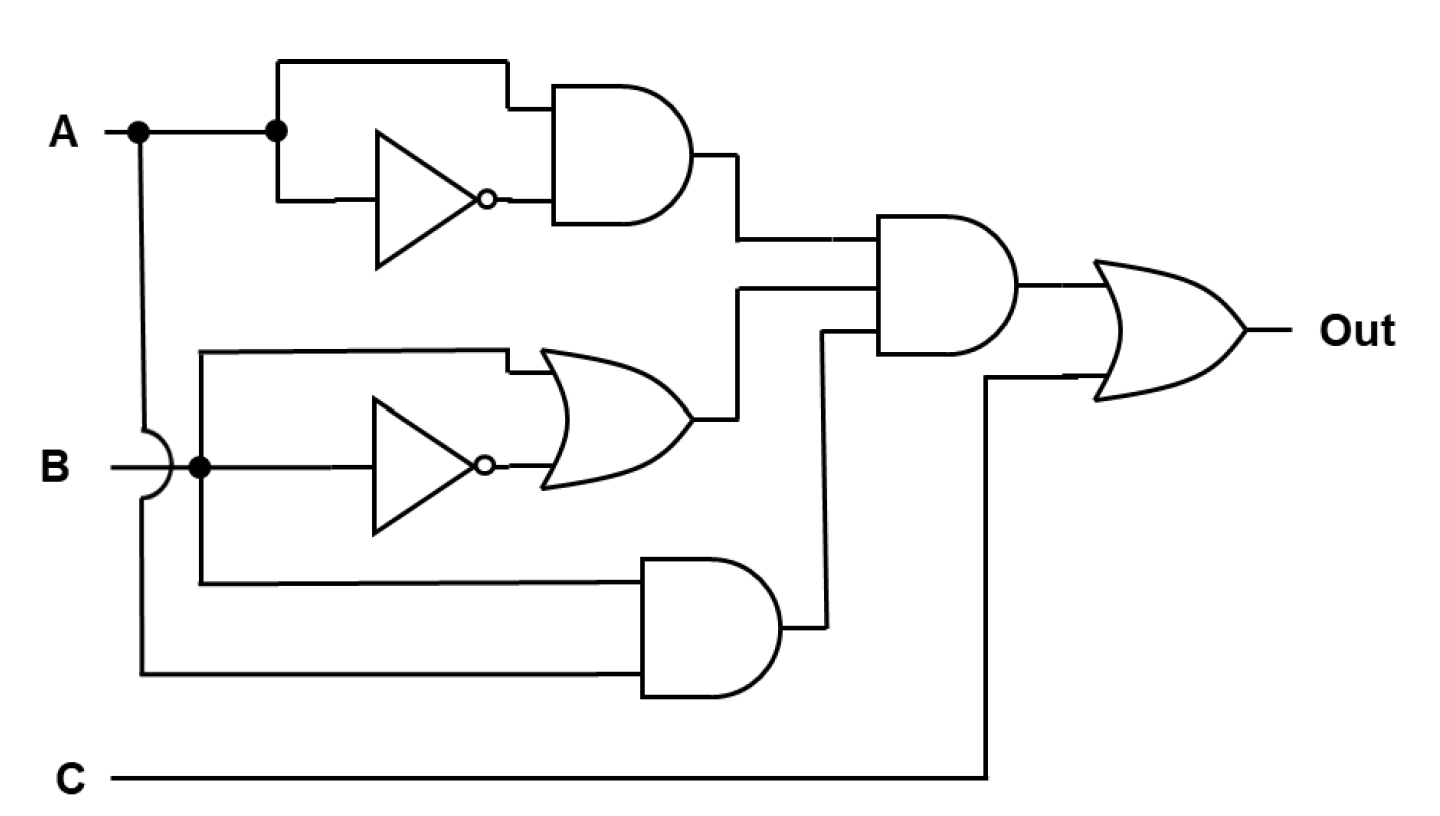
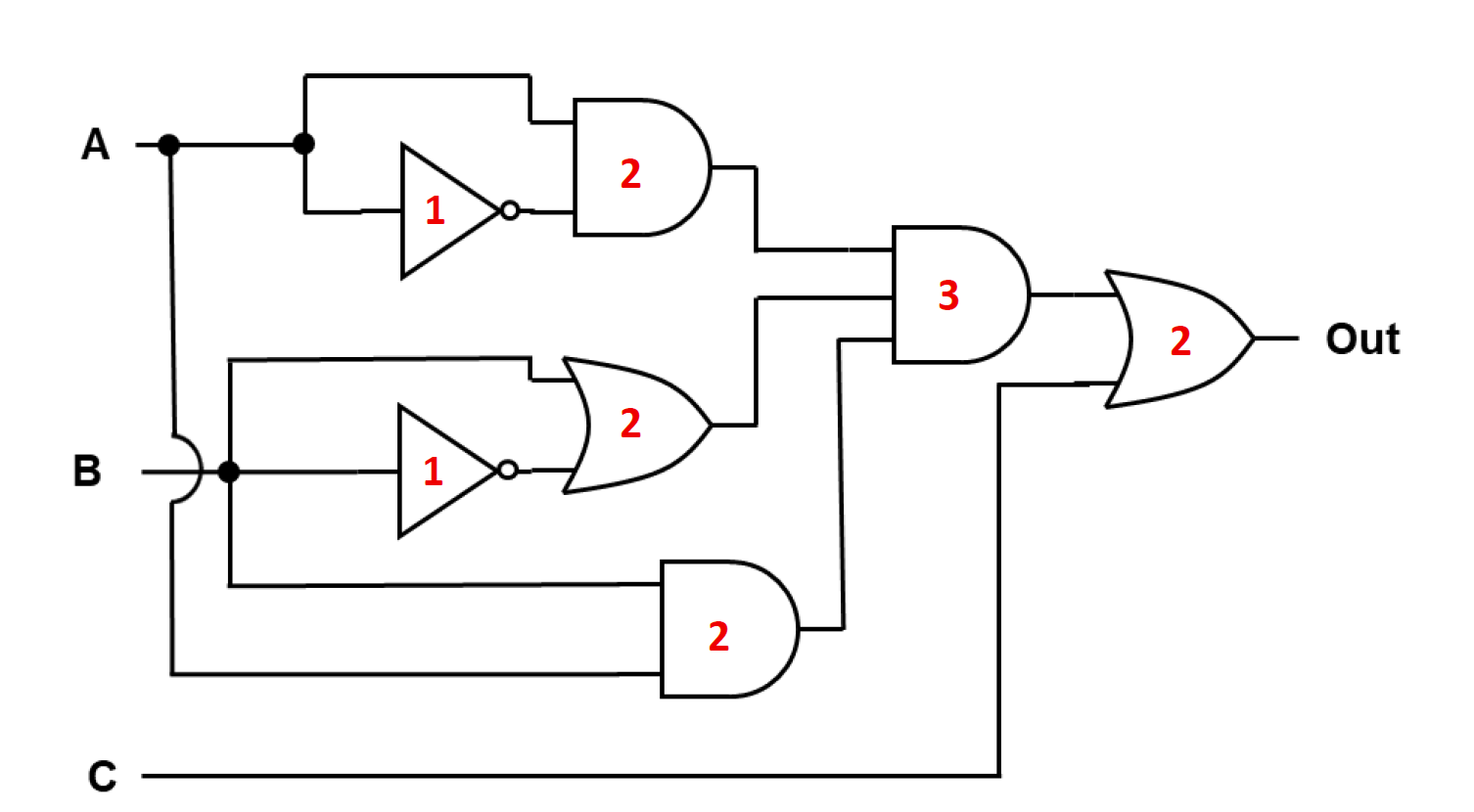
How many transistors does it take to build the following circuit?
Given the logic diagram, fill in the truth table.
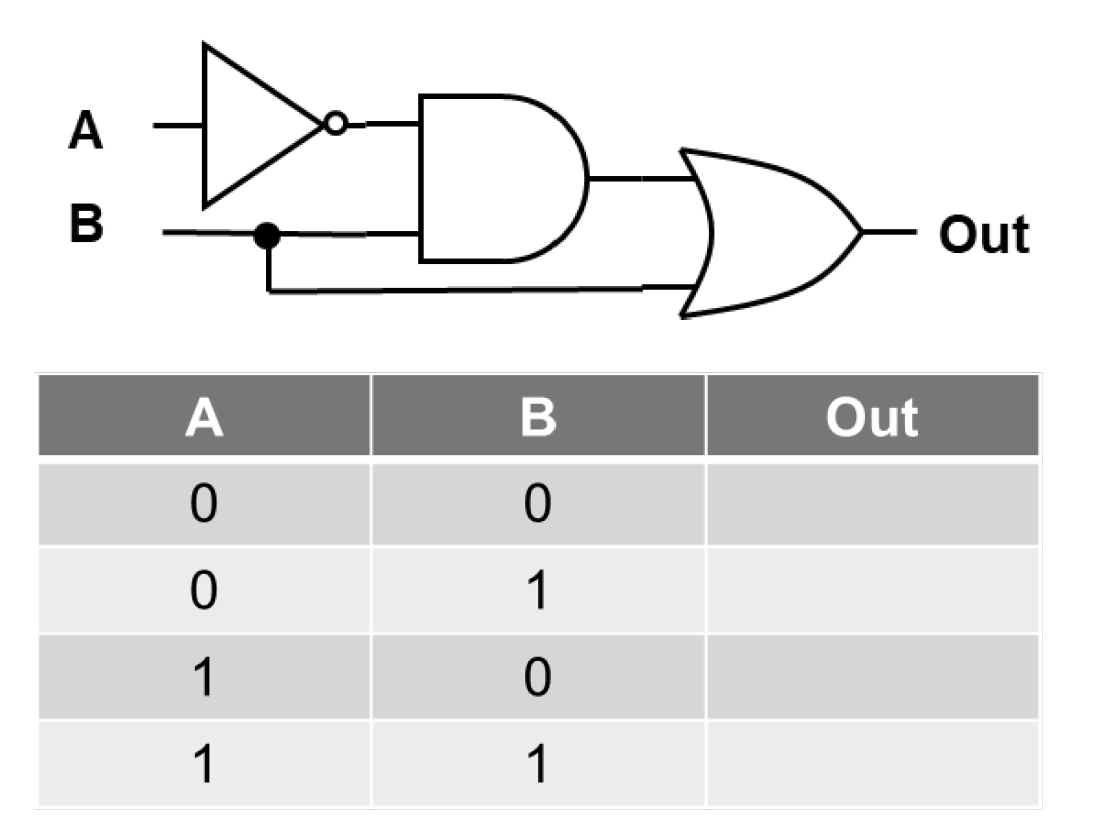
Since input \(B\) feeds directly into the OR gate, whenever \(B = 1\), the output must be \(1\), regardless of the value of \(A\).
When \(B = 0\), the output depends on the AND gate. However, the AND gate can only produce a \(1\) when both of its inputs are \(1\). Therefore, the AND gate outputs \(1\) only when \(A = 1\) and \(B = 1\).
Use this reasoning to complete each row of the truth table systematically.
\(A\) |
\(B\) |
Out |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
For the logic diagram below, build and complete the corresponding truth table.
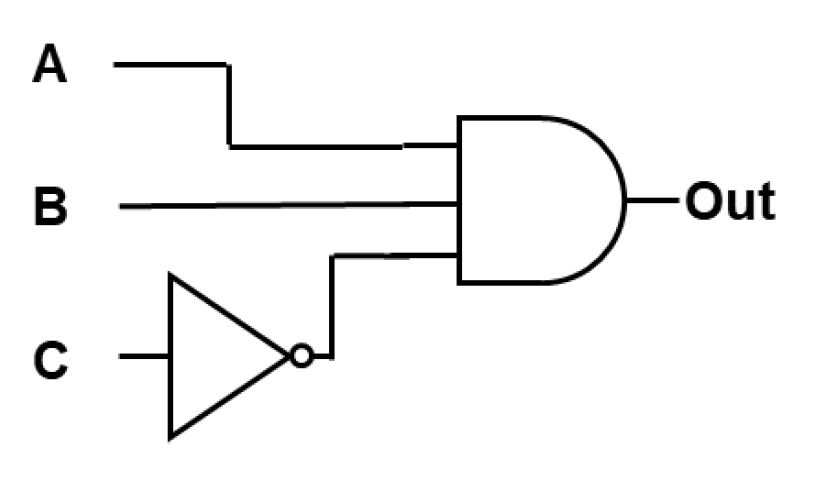
Since the circuit has three independent inputs (\(A\), \(B\), and \(C\)), there are:
possible input combinations, so the truth table must contain 8 rows.
Because the final gate before the output is an AND gate, the output can only be 1 if all inputs to that AND gate are 1. Tracing the circuit shows that this occurs only when:
\(A = 1\)
\(B = 1\)
\(C = 0\)
For all other input combinations, at least one input to the final AND gate is 0, which forces the output to 0.
Use this reasoning to complete each row of the truth table.
\(A\) |
\(B\) |
\(C\) |
Out |
|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
For the logic diagram below, complete the corresponding truth table.
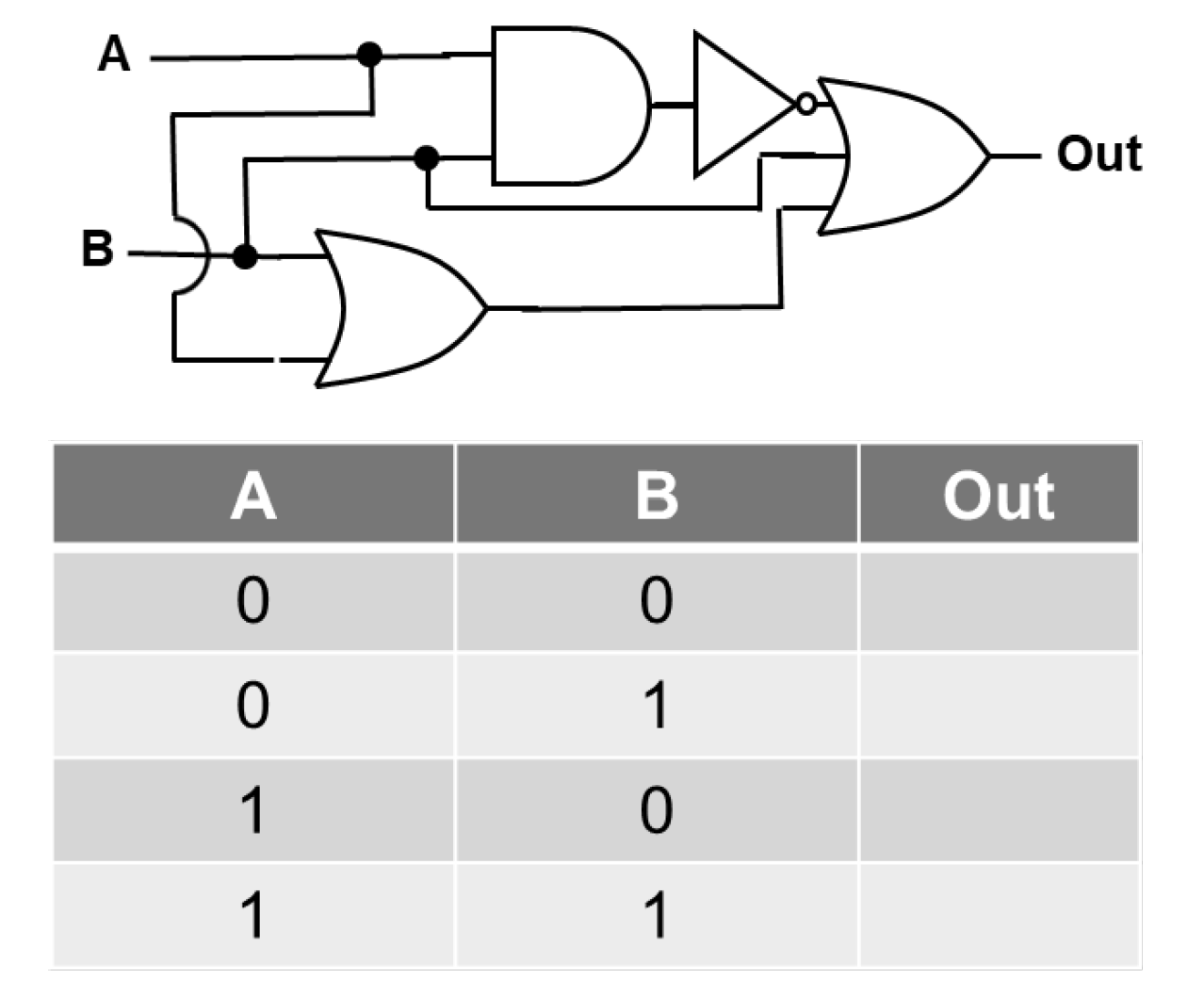
Since the final gate is an OR gate, the output will be 1 whenever either of its inputs is 1.
Notice that input \(B\) feeds directly into the final OR gate. Therefore, whenever \(B = 1\), the output must be 1, regardless of the value of \(A\).
Now consider the other input to the OR gate. It comes from an AND gate followed by a NOT gate. This means:
First, the AND gate evaluates \(A\) and \(B\).
Then, its output is inverted before reaching the OR gate.
If the AND gate outputs 0, the NOT gate changes it to 1. That 1 then forces the OR gate output to 1.
The AND gate only outputs 1 when both \(A = 1\) and \(B = 1\). In every other case, the AND gate outputs 0, which becomes 1 after the NOT gate.
Therefore, the output is 1 when:
\(B = 1\), or
the AND gate output is 0 (which occurs whenever \(A\) and \(B\) are not both 1).
Use this step-by-step reasoning to fill in the truth table.
\(A\) |
\(B\) |
Out |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
