Practice Problems (KEY)

Practice Problems (KEY)#

Plot the following equations:

a)
\(v(t) = -2 + 2\cos(360^\circ \cdot 100\ \mathrm{Hz} \cdot t)\ \mathrm{mV}\)

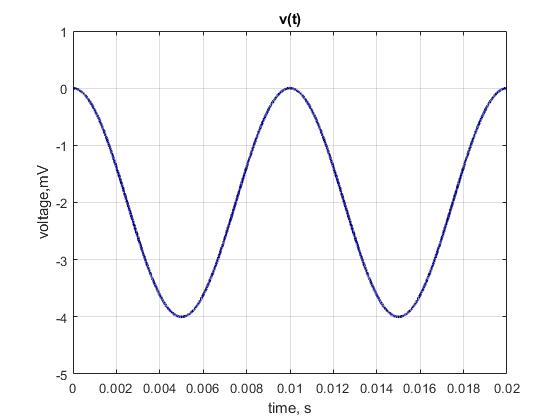
b)
\(v(t) = 2\cos(360^\circ \cdot 10\ \mathrm{Hz} \cdot t)\ \mathrm{V}\)

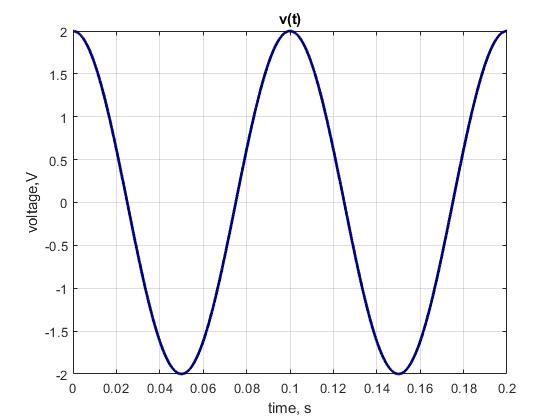
c)
\(v(t) = 4\cos(360^\circ \cdot 1\ \mathrm{kHz} \cdot t)\ \mathrm{mV}\)

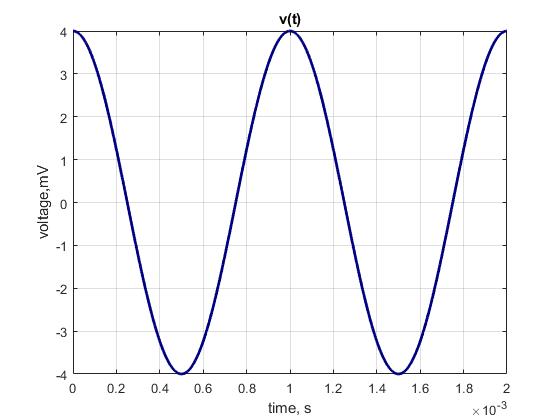
d)

What equation is associated with the graph?

\[ v(t) = 2\,\text{V} + \cos(360^\circ \cdot 10\,\text{kHz} \cdot t)\,\text{V} \]

e)

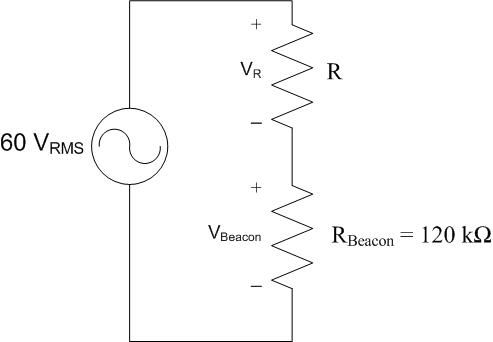
What equation is associated with the graph?

\[ v(t) = \cos(360^\circ \cdot 400\,\text{kHz} \cdot t)\,\text{mV} \]

If
\(v_{S}(t) = 4 + 8\cos(360^\circ \cdot 10\ \mathrm{kHz} \cdot t)\ \mathrm{V}\),
graph \(i_{X}(t)\) for the signal below.

The current is given by Ohm’s Law:

\[ i_X(t) = \frac{v_S(t)}{R_{\text{eq}}} \]

Substitute the source voltage and equivalent resistance:

\[ i_X(t) = \frac{4 + 8\cos(360^\circ \cdot 10\,\text{kHz} \cdot t)}{400\,\Omega} \]

Simplifying,

\[ i_X(t) = 0.01 + 0.02\cos(360^\circ \cdot 10\,\text{kHz} \cdot t)\,\text{A} \]

or, expressed in milliamps,

\[ i_X(t) = 10 + 20\cos(360^\circ \cdot 10\,\text{kHz} \cdot t)\,\text{mA} \]

Find the power consumed by the circuit below given \(V_{S} = 1.5\ \mathrm{V}\).

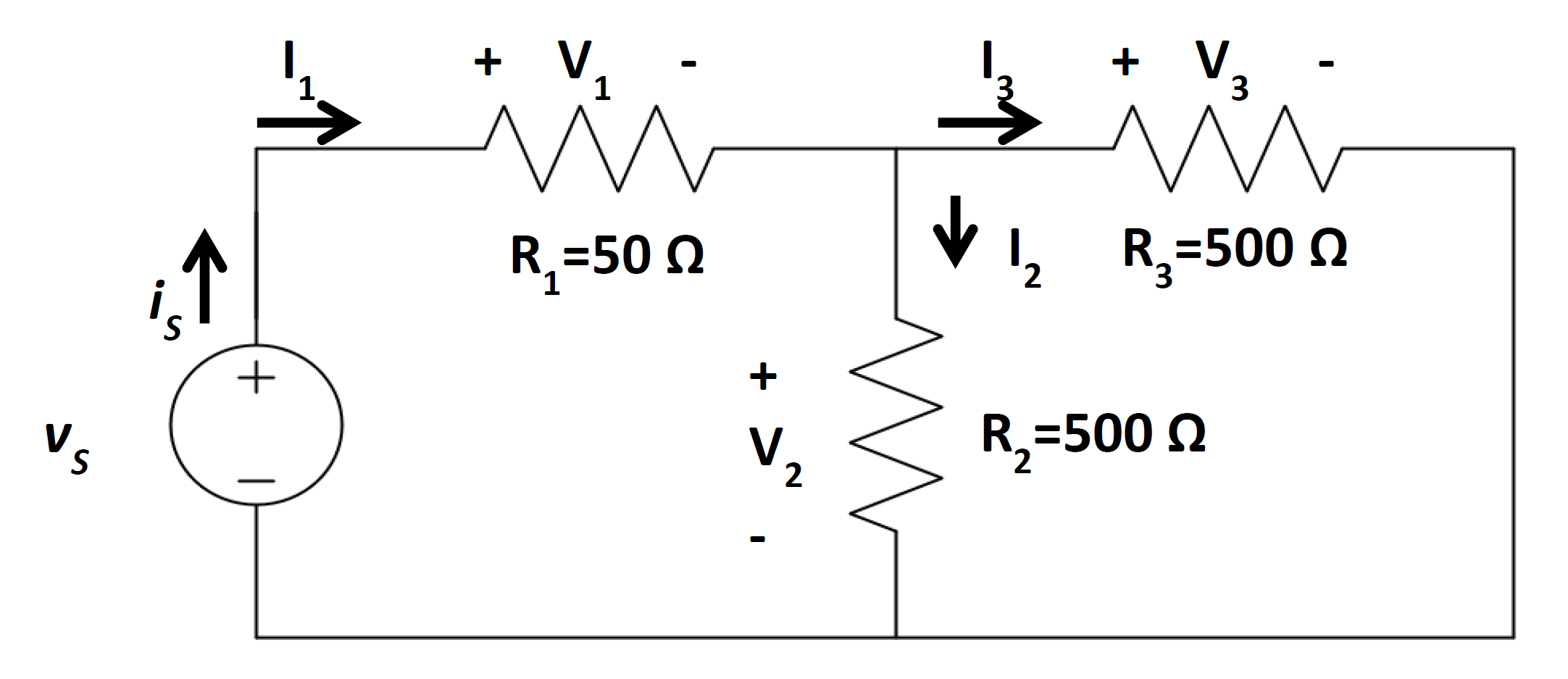
The equivalent resistance is

\[ R_{\text{eq}} = (R_3 \parallel R_2) + R_1 \]

\[ R_{\text{eq}} = \left( \frac{1}{\frac{1}{500\,\Omega} + \frac{1}{500\,\Omega}} \right) + 50\,\Omega = 300\,\Omega \]

The source current is

\[ I_S = \frac{V_S}{R_{\text{eq}}} = \frac{1.5\,\text{V}}{300\,\Omega} = 5\,\text{mA} \]

The total power supplied is

\[ P_{\text{tot}} = I_S V_S = (0.005\,\text{A})(1.5\,\text{V}) = 7.5\,\text{mW} \]

Find the average power consumed by the circuit below given:

The source voltage is given by

\[ v_S(t) = 2.12\cos\!\left(360^\circ \cdot 100\,\text{kHz} \cdot t\right)\,\text{V} \]

The source current is

\[ i_S(t) = \frac{v_S(t)}{R_{\text{eq}}} = \frac{2.12\cos\!\left(360^\circ \cdot 100\,\text{kHz} \cdot t\right)\,\text{V}}{300\,\Omega} \]

\[ i_S(t) = 7.07\cos\!\left(360^\circ \cdot 100\,\text{kHz} \cdot t\right)\,\text{mA} \]

The RMS current is

\[ I_{\text{RMS}} = \frac{7.07}{\sqrt{2}} = 5\,\text{mA} \]

The RMS voltage is

\[ V_{\text{RMS}} = \frac{2.12}{\sqrt{2}} = 1.5\,\text{V} \]

The average power consumed is

\[ P_{\text{AVG}} = V_{\text{RMS}} I_{\text{RMS}} = (1.5\,\text{V})(5\,\text{mA}) = 7.5\,\text{mW} \]

Compare the power consumed by the two circuits above.
The power consumed is the same.

What is \(\frac{1}{\mathrm{Hz}}\) equivalent to?

a. s - Correct Answer b. 1/s
c. f
d. None of the above

A 9 V battery is connected to a resistor that consumes 7.22 mW of power. Which AC source would cause the same resistor to consume 7.22 mW of average power?

a. \(7.22\cos\!\left(360^\circ \cdot 2\,\text{kHz} \cdot t\right)\,\text{mV}\)

b. \(9\cos\!\left(360^\circ \cdot 2\,\text{kHz} \cdot t\right)\,\text{V}\)

c. \(7.22\,\text{mV}_{\text{RMS}}\)

d. \(9\,\text{V}_{\text{RMS}}\) - Correct Answer

A B-52 generator produces the signal
\(v(t) = 290\cos(360^\circ \cdot 400\ \mathrm{Hz} \cdot t)\ \mathrm{V}\).

a) Graph the signal as a function of time.

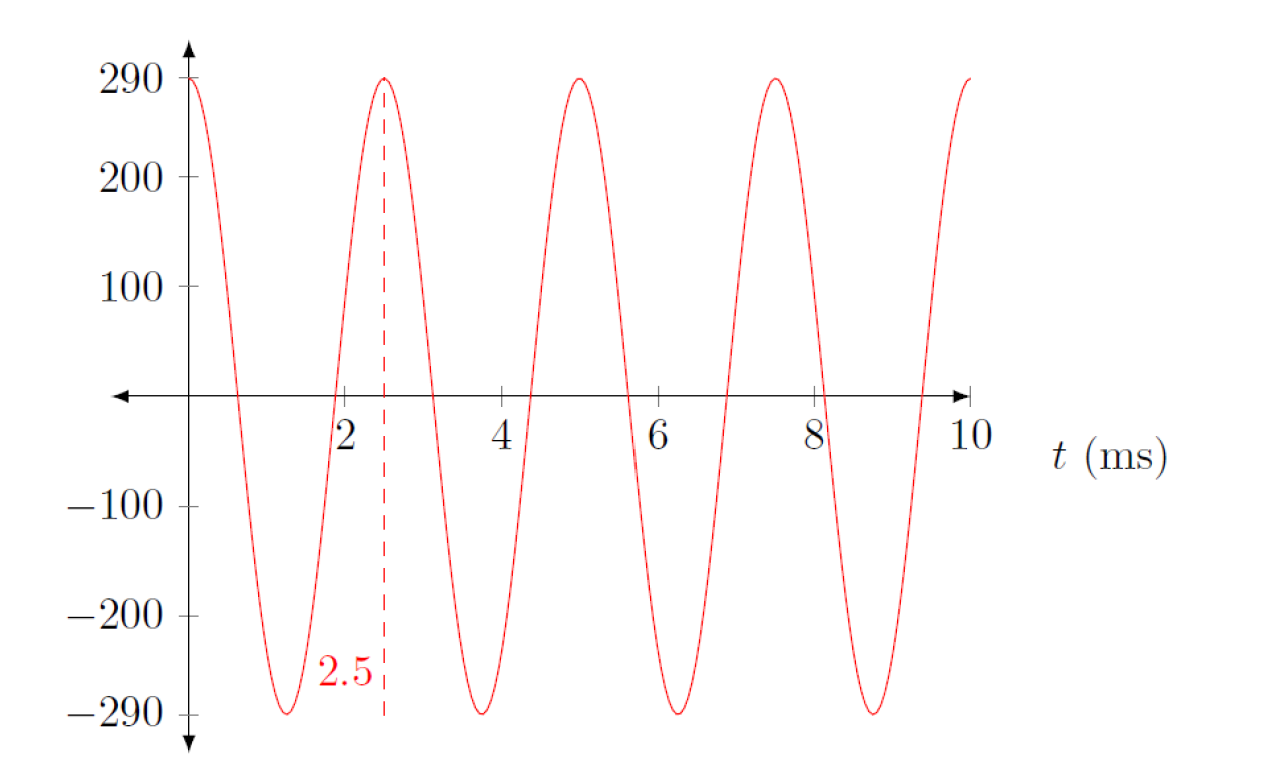
b) What is the RMS voltage for the generator?

Solution:

The amplitude of the signal is \(A = 290\,\text{V}\). Recall the RMS formula for a sinusoidal signal with a possible DC bias:

\[ V_{\text{RMS}} = \sqrt{V_{\text{bias}}^{2} + \frac{A^{2}}{2}} \]

In this case, \(V_{\text{bias}} = 0\), so the expression simplifies to:

\[ V_{\text{RMS}} = \frac{A}{\sqrt{2}} \]

Substituting the given amplitude:

\[ V_{\text{RMS}} = \frac{290\,\text{V}}{\sqrt{2}} = 205\,\text{V}_{\text{RMS}} \]

The fuse for a 2000-lb general-purpose bomb includes a spinner producing
\(v(t) = 15\cos(360^\circ \cdot 2\ \mathrm{kHz} \cdot t)\ \mathrm{mV}\).
The arming circuit is modeled as three resistors. Graph the current signal \(I_{S}(t)\).

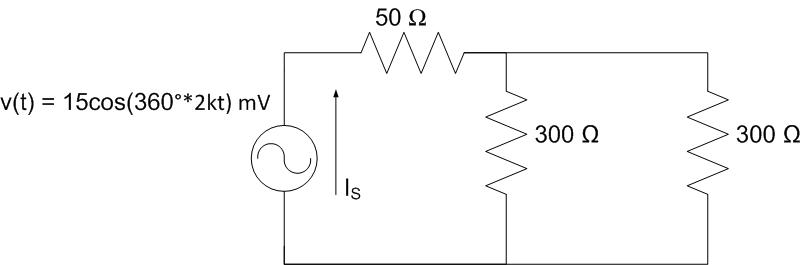
Solution:

To determine the current out of the spinner, we must first find the equivalent resistance of the circuit. The equivalent resistance is:

\[ R_{\text{EQ}} = (300\,\Omega \parallel 300\,\Omega) + 50\,\Omega = 200\,\Omega \]

Therefore, the equivalent circuit is a single resistor of \(200\,\Omega\) driven by the source

\[ v(t) = 15\cos\!\left(360^\circ \cdot 2\,\text{kHz} \cdot t\right)\,\text{mV}. \]

Now, we find the source current \(I_S(t)\) using Ohm’s Law:

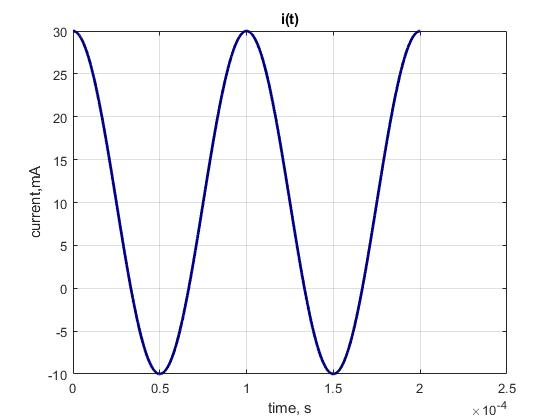
\[ I_S(t) = \frac{v(t)}{R_{\text{EQ}}} = \frac{15\cos\!\left(360^\circ \cdot 2\,\text{kHz} \cdot t\right)\,\text{mV}}{200\,\Omega} \]

\[ I_S(t) = 75\cos\!\left(360^\circ \cdot 2\,\text{kHz} \cdot t\right)\,\mu\text{A} \]

Using this result, we can easily graph the current signal. Since there is no phase shift (i.e., \(\phi = 0\)), the period of the signal is

\[ T = \frac{1}{f} = \frac{1}{2000\,\text{Hz}} = 500\,\mu\text{s}. \]

The resulting waveform for \(I_S(t)\) is a cosine signal with a peak amplitude of \(75\,\mu\text{A}\) and a period of \(500\,\mu\text{s}\).

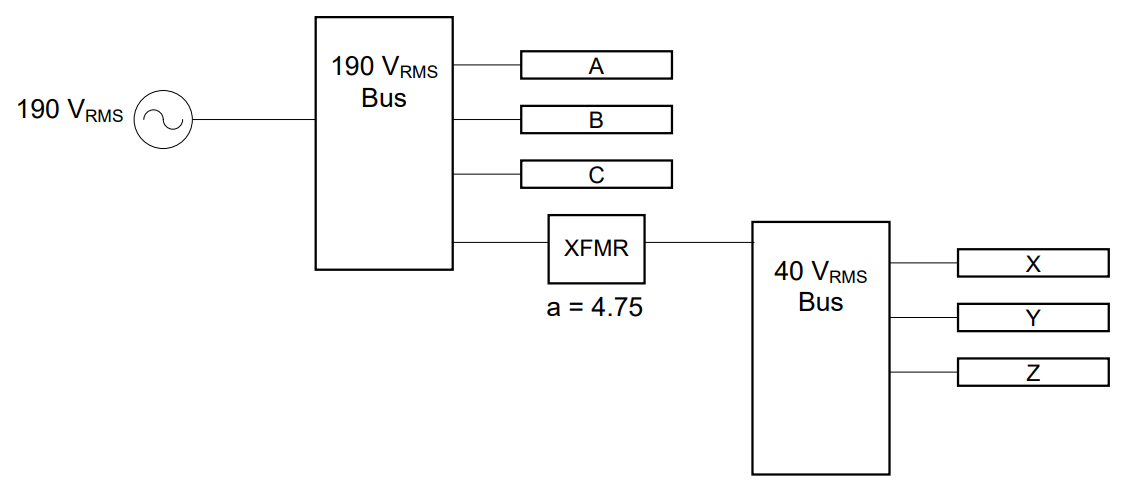
Which of the two sources below produces more average power?

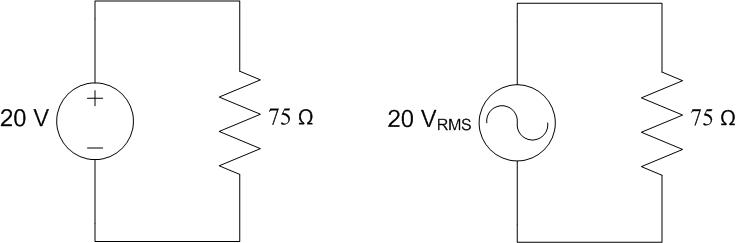
Solution:
In the circuits above, we have a DC source and an AC source. The DC source is \(20\,\text{V}\), and the AC source is \(20\,\text{V}_{\text{RMS}}\). Both sources are connected in parallel with a \(75\,\Omega\) resistor.

We know that the power supplied equals the power consumed.

For a DC source, the power delivered to a resistive load is given by:

\[ P = VI = \frac{V^2}{R} = I^2 R \]

For an AC source, the average power delivered to a resistive load is given by the same expressions, except that RMS values are used instead of peak values:

\[ P_{\text{avg}} = V_{\text{RMS}} I_{\text{RMS}} = \frac{V_{\text{RMS}}^2}{R} = I_{\text{RMS}}^2 R \]

Since the RMS value of an AC source is the DC-equivalent value in terms of power delivery, a \(20\,\text{V}\) DC source and a \(20\,\text{V}_{\text{RMS}}\) AC source deliver the same average power to the same resistive load.

Therefore, the two sources supply identical average power to the \(75\,\Omega\) resistor.

The circuit below has a current source providing
\(i(t) = 11.75\cos(360^\circ \cdot 50\ \mathrm{Hz} \cdot t)\ \mathrm{A}\).

Find \(v_{1}(t)\).

Solution:
If we can find the current through the \(6\,\Omega\) resistor, we can also find the voltage drop across it. In this circuit, all resistors are in parallel, so we can use a current divider to find the current through the \(6\,\Omega\) resistor.

Recall the current divider equation:

\[ I_x = \frac{R_{\text{eq}}}{R_x} I_{\text{Total}} \]

Here:

\(I_x\) is the current through the \(6\,\Omega\) resistor (denoted \(I_1\)),
\(R_x = 6\,\Omega\),
\(I_{\text{Total}} = i(t)\), the current provided by the source.

First, find the equivalent resistance of the parallel resistors:

\[ R_{\text{eq}} = \left( \frac{1}{6\,\Omega} + \frac{1}{10\,\Omega} + \frac{1}{8\,\Omega} \right)^{-1} = 2.553\,\Omega \]

Now substitute into the current divider equation:

\[ I_1(t) = \frac{2.553\,\Omega}{6\,\Omega} \left( 11.75\cos(360^\circ \cdot 50\,\text{Hz} \cdot t) \right) = 5\cos(360^\circ \cdot 50\,\text{Hz} \cdot t)\,\text{A} \]

Finally, use Ohm’s Law to find the voltage across the \(6\,\Omega\) resistor:

\[ v_1(t) = I_1(t)\,R = \left(5\cos(360^\circ \cdot 50\,\text{Hz} \cdot t)\right)(6\,\Omega) \]

\[ v_1(t) = 30\cos(360^\circ \cdot 50\,\text{Hz} \cdot t)\,\text{V} \]

An AC-powered electric fan, modeled as a 150 \(\Omega\) resistor, is plugged into a \(120\ \mathrm{V}_{RMS}\) outlet. The fan requires \(90\ \mathrm{V}_{RMS}\) to operate, so a resistor is added to form a voltage divider.

Given:

\(V_{S} = 120\ \mathrm{V}_{RMS}\)
\(R_{fan} = 150\ \Omega\)

Find the resistor value \(R\) to provide the fan with \(90\ \mathrm{V}_{RMS}\).

Solution:
The resistor \(R_{\text{adapter}}\) will drop some of the voltage, but we first need to determine its value. We can find this using the voltage divider equation.

\[ V_{\text{fan}} = V_S \frac{R_{\text{fan}}}{R_{\text{adapter}} + R_{\text{fan}}} \]

In this case, we know

\[ V_{\text{fan}} = 90~\text{V}_{\text{RMS}}, \quad V_S = 120~\text{V}_{\text{RMS}}, \quad R_{\text{fan}} = 150~\Omega \]

We solve the voltage divider equation for \(R_{\text{adapter}}\):

\[ R_{\text{adapter}} = R_{\text{fan}} \frac{V_S - V_{\text{fan}}}{V_{\text{fan}}} \]

Substituting values,

\[ R_{\text{adapter}} = 150~\Omega \left( \frac{120~\text{V}_{\text{RMS}} - 90~\text{V}_{\text{RMS}}} {90~\text{V}_{\text{RMS}}} \right) = 50~\Omega \]

Therefore,

\[ R = 50~\Omega \]