Practice Problems (KEY)

Practice Problems (KEY)#

Problem 1#

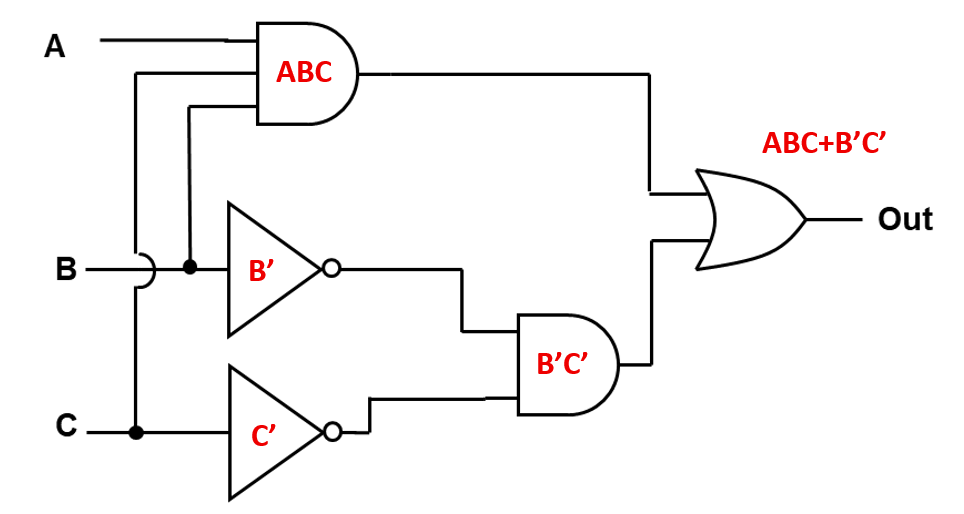
Express the logic diagram as a Boolean equation. Practice Problem 1 – Logic Diagram

Problem 2#

Construct a truth table from the following Boolean equation

\[ F = A'B'C' + AB + BC' \]

Two Methods for Constructing the Truth Table#

Given the Boolean expression:

\[ F = A'B'C' + AB + BC' \]

Method 1 — Term Matching (Minterm Identification)#

Place a 1 in the truth table for any row that satisfies one of the product terms:

  • \(A'B'C'\) → corresponds to \((A,B,C) = (0,0,0)\)

  • \(AB\) → corresponds to \((A,B) = (1,1)\) (for either value of \(C\))

  • \(BC'\) → corresponds to \((B,C) = (1,0)\) (for either value of \(A\))

All other rows receive a 0.

\(A\)

\(B\)

\(C\)

\(\text{Out}\)

0

0

0

\(A'B'C' = 1\)

0

0

1

0

0

1

0

\(BC' = 1\)

0

1

1

0

1

0

0

0

1

0

1

0

1

1

0

\(AB \text{ or } BC' = 1\)

1

1

1

\(AB = 1\)

Method 2 — Direct Substitution#

For each row of the truth table:

  1. Substitute the values of \(A\), \(B\), and \(C\) into
    $\( F = A'B'C' + AB + BC' \)$

  2. Evaluate each product term using Boolean multiplication.

  3. OR the resulting values to determine the final output.

\(A\)

\(B\)

\(C\)

\(\text{Out}\)

0

0

0

\(1\cdot1\cdot1 + 0\cdot0 + 1\cdot0 = 1\)

0

0

1

\(1\cdot1\cdot0 + 0\cdot0 + 0\cdot0 = 0\)

0

1

0

\(1\cdot0\cdot1 + 0\cdot1 + 1\cdot1 = 1\)

0

1

1

\(1\cdot0\cdot0 + 1\cdot0 + 1\cdot0 = 0\)

1

0

0

\(0\cdot1\cdot1 + 1\cdot0 + 0\cdot1 = 0\)

1

0

1

\(0\cdot1\cdot0 + 1\cdot0 + 0\cdot0 = 0\)

1

1

0

\(0\cdot0\cdot1 + 1\cdot1 + 1\cdot1 = 1\)

1

1

1

\(0\cdot0\cdot0 + 1\cdot1 + 1\cdot0 = 1\)

Problem 3#

Given the truth table, create a Boolean equation (do not simplify)

\(A\)

\(B\)

\(C\)

\(\text{Out}\)

SOP Term

0

0

0

1

\(A'B'C'\)

0

0

1

0

0

1

0

1

\(A'BC'\)

0

1

1

0

1

0

0

1

\(AB'C'\)

1

0

1

0

1

1

0

1

\(ABC'\)

1

1

1

1

\(ABC\)
\[ \text{Out} = A'B'C' + A'BC' + AB'C' + ABC' + ABC \]

Problem 4#

For the logic diagram below, create a Boolean equation, simplify, and then fill out the truth table Practice Problem 4 – Logic Diagram and Table

\[ \text{Out} = (AB)' + B + (A + B) \]

Rearrange terms:

\[ \text{Out} = (AB)' + B + B + A \]

Apply Identity 3:

\[ B + B = B \]
\[ \text{Out} = (AB)' + A + B \]

Apply Identity 10b (DeMorgan’s Law):

\[ (AB)' = A' + B' \]
\[ \text{Out} = A' + B' + A + B \]

Rearrange:

\[ \text{Out} = A + A' + B + B' \]

Apply Identity 4:

\[ A + A' = 1 \]
\[ B + B' = 1 \]
\[ \text{Out} = 1 + 1 \]

Apply Boolean addition rule:

\[ 1 + 1 = 1 \]
\[ \boxed{\text{Out} = 1} \]

\(A\)

\(B\)

\(\text{Out}\)

0

0

1

0

1

1

1

0

1

1

1

1

Problem 5#

Given the truth table, create a Boolean equation, simplify, and then create a logic diagram. Hint: This simplifies to 1 NOT, 1 AND, and 2 OR.

\(A\)

\(B\)

\(C\)

\(\text{Out}\)

SOP Term

0

0

0

1

\(A'B'C'\)

0

0

1

1

\(A'B'C\)

0

1

0

0

0

1

1

0

1

0

0

0

1

0

1

0

1

1

0

1

\(ABC'\)

1

1

1

1

\(ABC\)
\[ \text{Out} = A'B'C' + A'B'C + ABC' + ABC \]

Factor using Identity 9a:

\[ \text{Out} = A'B'(C' + C) + ABC' + ABC \]

Apply Identity 4:

\[ C' + C = 1 \]
\[ \text{Out} = A'B' + ABC' + ABC \]

Factor using Identity 9a:

\[ \text{Out} = A'B' + AB(C' + C) \]

Apply Identity 4:

\[ C' + C = 1 \]
\[ \text{Out} = A'B' + AB \]

Apply Identity 10a (DeMorgan’s Law):

\[ A'B' = (A + B)' \]
\[ \boxed{\text{Out} = (A + B)' + AB} \]

Practice Problem 4 – Logic Diagram and Table

Contents