Practice Problems#
Problem 1#
Express the logic diagram as a Boolean equation.
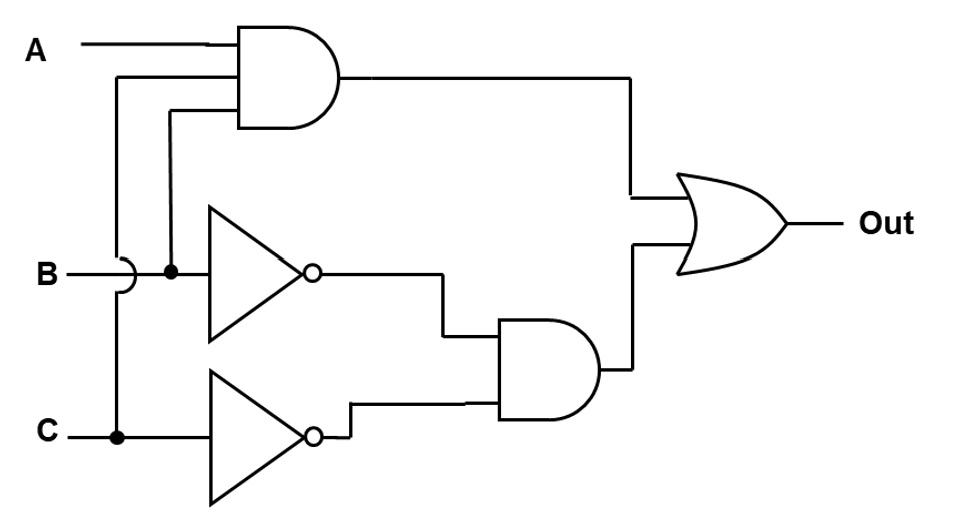
Problem 2#
Construct a truth table from the following Boolean equation
\[
F = A'B'C' + AB + BC'
\]
Problem 3#
Given the truth table, create a Boolean equation (do not simplify)
\(A\) |
\(B\) |
\(C\) |
\(\text{Out}\) |
|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Problem 4#
For the logic diagram below, create a Boolean equation, simplify, and then fill out the truth table
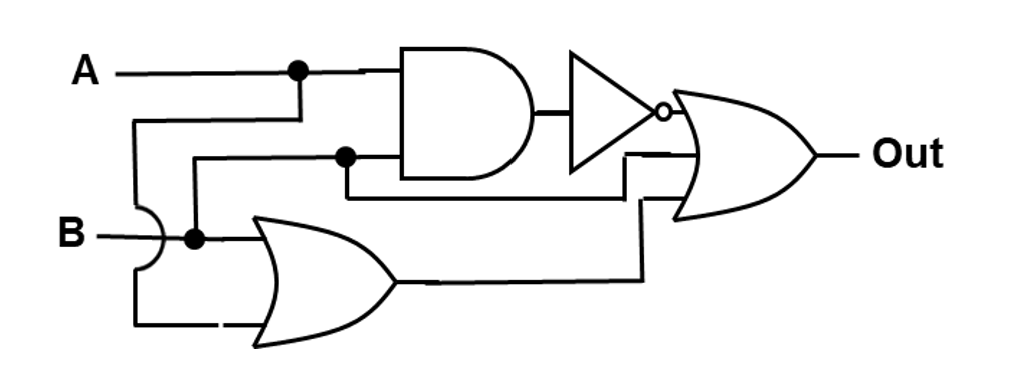
\(A\) |
\(B\) |
\(\text{Out}\) |
|---|---|---|
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
Problem 5#
Given the truth table, create a Boolean equation, simplify, and then create a logic diagram. Hint: This simplifies to 1 NOT, 1 AND, and 2 OR.
\(A\) |
\(B\) |
\(C\) |
\(\text{Out}\) |
|---|---|---|---|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
