Practice Problems (KEY)
You’ve just finished a major upgrade to your garage where you installed an industrial-grade lathe. The lathe’s motor is rated to be 88% efficient under rated conditions and is capable of outputting 550 W. You plug it into the wall (a standard \(120\ \mathrm{V}_{RMS}\) wall socket) and start using it, only to have the power go out as soon as you start cutting. When you look in your circuit breaker box, you find that the 5 A breaker for the garage popped. Why?

\[
\eta = \frac{P_{out}}{P_{in}} \cdot 100, \qquad
P_{in} = \frac{P_{out}}{\eta/100} = \frac{550\ \mathrm{W}}{0.88} = 625\ \mathrm{W}
\]
\[
I_{S,\mathrm{RMS}} = \frac{P_{in}}{V_{S,\mathrm{RMS}}}
= \frac{625\ \mathrm{W}}{120\ \mathrm{V}_{RMS}}
= 5.2\ \mathrm{A}_{RMS} > 5.0\ \mathrm{A\ (CB\ rating)}
\]
You are researching home standby generator systems which automatically take over if the power goes out. You determine that you can survive with the following appliances: refrigerator (1.2 kW), oven (1.8 kW), and microwave (800 W). Will you be able to run these appliances and the central air conditioning (5.2 kW) with a 7 kW generator or will you need to upgrade to the more expensive 12 kW version?
\[
P_{load} = P_{refrig} + P_{oven} + P_{microwave} + P_{AC}
\]
\[
P_{load} = 1.2\ \mathrm{kW} + 1.8\ \mathrm{kW} + 0.8\ \mathrm{kW} + 5.2\ \mathrm{kW} = 9\ \mathrm{kW}
\]
Must upgrade to the 12 kW generator to accommodate the entire load.
An AC-powered rotating beacon, modeled as a \(120 \mathrm{k}\Omega}\) resistor, is to be installed on an aircraft. Since the beacon requires \(55\ \mathrm{V}_{RMS}\) to operate, a resistor is placed in series to act as a voltage divider. The aircraft generator produces a voltage of
\(v(t) = 84.85\cos(360^\circ \cdot 400t)\ \mathrm{V}\).
If the required efficiency for this circuit is 85%, is this a viable option?
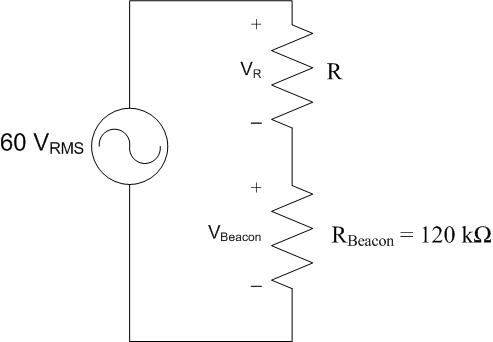
\[
V_{S,\mathrm{RMS}} = \frac{84.85\ \mathrm{V}}{\sqrt{2}} = 60\ \mathrm{V}_{RMS}
\]
\[
V_{R} = V_{S} - V_{Beacon} = 60\ \mathrm{V}_{RMS} - 55\ \mathrm{V}_{RMS} = 5\ \mathrm{V}_{RMS}
\]
\[
I_{S,\mathrm{RMS}} = I_{Beacon} = \frac{V_{Beacon}}{R_{Beacon}}
= \frac{55\ \mathrm{V}_{RMS}}{120\ \mathrm{k}\Omega}
= 458\ \mu\mathrm{A}_{RMS}
\]
\[
P_{loss} = V_{R} I_{S}
= (5\ \mathrm{V}_{RMS})(458 \times 10^{-6}\ \mathrm{A}_{RMS})
= 2.29\ \mathrm{mW}
\]
\[
P_{useful} = V_{Beacon} I_{S}
= (55\ \mathrm{V}_{RMS})(458 \times 10^{-6}\ \mathrm{A}_{RMS})
= 25.2\ \mathrm{mW}
\]
\[
\eta = \frac{P_{useful}}{P_{wasted} + P_{useful}} \cdot 100
= \frac{25.2\ \mathrm{mW}}{2.29\ \mathrm{mW} + 25.2\ \mathrm{mW}} \cdot 100
= 91.7\%
\]
Yes, this circuit is a viable option because \(91.7\% > 85\%\).
This is the same problem as an example problem in the reading, with the exception that the voltage across the beacon is 40 \( \mathrm{V}_{RMS} \) in the reading. In the reading, the efficiency of the circuit is 66.67% because the voltage drop across the beacon is less.
This helps us explore a few edge cases. If the voltage drop across the beacon was almost 0 \( \mathrm{V}_{RMS} \), then the efficiency would be nearly 0%. On the other hand, if the voltage drop across the beacon was nearly 60 \( \mathrm{V}_{RMS} \), then the efficiency would be nearly 100%. Since the same current flows through all devices in this series circuit, the voltage drop across the devices determines the power consumed by the devices and, therefore, the efficiency of the circuit.
A generator is responsible for powering the scenario below. What efficiency must it be rated for so it can provide enough power?

\[
R_{eq} =
\left(\frac{1}{20\ \Omega} + \frac{1}{10\ \Omega} + \frac{1}{7\ \Omega + 8\ \Omega}\right)^{-1}
= 4.62\ \Omega
\]
\[
P_{load} = \frac{V_{gen}^{2}}{R_{eq}}
= \frac{(115\ \mathrm{V}_{RMS})^{2}}{4.62\ \Omega}
= 2.86\ \mathrm{kW}
= P_{out,gen}
\]
\[
\eta = \frac{P_{out,gen}}{P_{in,gen}} \cdot 100
= \frac{2.86\ \mathrm{kW}}{3\ \mathrm{kW}} \cdot 100
= 95.3\%
\]
A 2 hp motor is plugged into a standard wall outlet. Its efficiency is 90%. What current and power does it draw from the wall outlet?

\[
P_{out} = 2\ \mathrm{hp}\left(\frac{745.7\ \mathrm{W}}{1\ \mathrm{hp}}\right) = 1491.4\ \mathrm{W}
\]
\[
\eta = \frac{P_{out}}{P_{in}} \cdot 100, \qquad
P_{in} = \frac{P_{out}}{\eta/100} = \frac{1491.4\ \mathrm{W}}{0.9} = 1.66\ \mathrm{kW}
\]
\[
I_{S,\mathrm{RMS}} = \frac{P_{in}}{V_{S,\mathrm{RMS}}}
= \frac{1.66\ \mathrm{kW}}{120\ \mathrm{V}_{RMS}}
= 13.8\ \mathrm{A}_{RMS}
\]
Answer the following questions for the circuit below.
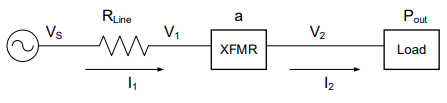
a. Draw the circuit above as a block diagram.
b. Find \(V_{gen}\), \(P_{gen}\), and \(\eta\) for the circuit above.
\[
I_{2} = \frac{P_{House}}{V_{house}} = \frac{1500\ \mathrm{W}}{120\ \mathrm{V}_{RMS}} = 12.5\ \mathrm{A}_{RMS}
\]
\[
a = \frac{I_{2}}{I_{1}}, \qquad I_{1} = \frac{I_{2}}{a} = \frac{12.5\ \mathrm{A}}{10} = 1.25\ \mathrm{A}_{RMS}
\]
\[
I_{line} = I_{1}, \qquad
P_{line} = I_{line}^{2} R_{line} = (1.25\ \mathrm{A}_{RMS})^{2}(5\ \Omega) = 7.8125\ \mathrm{W}
\]
\[
P_{gen} = P_{house} + P_{line} = 1500\ \mathrm{W} + 7.8125\ \mathrm{W} = 1507.8125\ \mathrm{W}
\]
\[
\eta = \frac{P_{Useful}}{P_{Useful} + P_{Wasted}} \cdot 100
= \frac{P_{house}}{P_{house} + P_{line}} \cdot 100
= \frac{1500}{1500 + 7.8125} \cdot 100
= 99.48\%
\]
\[
V_{gen} = \frac{P_{gen}}{I_{1}} = \frac{1507.8125\ \mathrm{W}}{1.25\ \mathrm{A}_{RMS}} = 1.206\ \mathrm{kV}
\]
DC sources can be used with transformers.
(a) True (b) False
Why does our national power grid use AC power?
The key is to keep the current low over a transmission line to decrease power lost in the line. Transformers enable us to transmit power at very high voltages and low currents and then step down the voltage to more useful levels. This allows us to transmit the energy efficiently. Transformers only operate with AC power, so the efficiency improvements associated with transformers caused us to use AC power.
Given the ideal transformer below, answer the following questions.

a) Does this circuit contain a step up or step down transformer?
\[
a = \frac{N_{1}}{N_{2}} = \frac{V_{1}}{V_{2}} = \frac{5}{1} = 5 \quad \mathrm{(step\ down)}
\]
You can see that if you solve the above equation for \(V_{2}\), then \(V_{1}\) will be divided by 5, making \(V_{2} < V_{1}\).
b) What is the voltage across the primary coil of the transformer?
\(V_{S}\) is parallel with the primary side of the transformer, therefore
\(V_{1} = V_{S} = 200\ \mathrm{V}_{RMS}\).
c) What is the voltage across the secondary coil of the transformer?
\[
a = \frac{V_{1}}{V_{2}} \Rightarrow V_{2} = \frac{V_{1}}{a}
\]
\[
V_{2} = \frac{200\ \mathrm{V}_{RMS}}{5} = 40\ \mathrm{V}_{RMS}
\]
d) What is the current \(I_{2}\) at the secondary side of the transformer?
\[
R_{eq,secondary} = 4000\ \Omega + \left(\frac{1}{20000\ \Omega} + \frac{1}{5000\ \Omega}\right)^{-1}
= 8000\ \Omega
= 8\ \mathrm{k}\Omega
\]
\[
I_{2} = \frac{V_{2}}{R_{eq,secondary}} = \frac{40\ \mathrm{V}_{RMS}}{8\ \mathrm{k}\Omega} = 5\ \mathrm{mA}_{RMS}
\]
e) Assuming no power losses, how much average power is supplied by the source?
Since we are assuming no power losses, \(P_{S} = P_{Load}\).
\[
P_{S} = P_{Load} = V_{2} I_{2} = (40\ \mathrm{V}_{RMS})(0.005\ \mathrm{A}_{RMS}) = 0.2\ \mathrm{W} = 200\ \mathrm{mW}
\]
An in-room air conditioning unit requires \(30\ \mathrm{V}_{RMS}\) to operate. A transformer is used to step down the \(120\ \mathrm{V}_{RMS}\) provided by a standard wall outlet. What turns ratio should be used?
\[
a = \frac{V_{1}}{V_{2}} = \frac{120\ \mathrm{V}_{RMS}}{30\ \mathrm{V}_{RMS}} = 4
\]
A power plant provides power to a small community 300 km away. The resistance in the power line can be modeled as a \(10\ \Omega\) resistor. A transformer with a turns ratio of \(a = 70\) is used between the transmission line and the community.

a) If the community uses 123 kW of power at \(120\ \mathrm{V}_{RMS}\), how efficient is this system?
\[
I_{2} = \frac{P_{community}}{V_{2}} = \frac{123\ \mathrm{kW}}{120\ \mathrm{V}_{RMS}} = 1025\ \mathrm{A}_{RMS} = 1.025\ \mathrm{kA}_{RMS}
\]
\[
a = \frac{I_{2}}{I_{1}}, \qquad I_{1} = \frac{I_{2}}{a} = \frac{1.025\ \mathrm{kA}}{70} = 14.6\ \mathrm{A}_{RMS}
\]
\[
I_{line} = I_{1}, \qquad
P_{line} = I_{line}^{2} R_{line} = (14.6\ \mathrm{A}_{RMS})^{2}(10\ \Omega) = 2.14\ \mathrm{kW}
\]
\[
\eta = \frac{P_{useful}}{P_{wasted} + P_{useful}} \cdot 100
= \frac{P_{community}}{P_{line} + P_{community}} \cdot 100
= \frac{123}{2.14 + 123} \cdot 100
= 98.3\%
\]
b) How many volts does the power plant need to provide?
\[
V_{S} = \frac{P_{S}}{I_{1}} = \frac{123\ \mathrm{kW} + 2.14\ \mathrm{kW}}{14.6\ \mathrm{A}_{RMS}} = 8.57\ \mathrm{kV}
\]
c) A contractor has proposed replacing the transmission line with one having only 5 Ω of resistance. If everything else remains the same, how efficient would the improved system be?
\[
P_{line} = I_{line}^{2} R_{line} = (14.6\ \mathrm{A}_{RMS})^{2}(5\ \Omega) = 1.0658\ \mathrm{kW}
\]
\[
\eta = \frac{P_{community}}{P_{line} + P_{community}} \cdot 100
= \frac{123}{1.0658 + 123} \cdot 100
= 99.1\%
\]
The electrical distribution system for a deployed Main Operating Base (MOB) is shown below. The system provides an average of 150 kW of power at \(120\ \mathrm{V}_{RMS}\). The transmission line has a cumulative resistance of 2 \(\Omega\) and uses a transformer with a turns ratio of \(a = 8\). What are the source voltage and the efficiency of this system?

\[
I_{2} = \frac{P_{MOB}}{V_{2}} = \frac{150\ \mathrm{kW}}{120\ \mathrm{V}_{RMS}}
= 1250\ \mathrm{A}_{RMS} = 1.25\ \mathrm{kA}_{RMS}
\]
\[
a = \frac{I_{2}}{I_{1}}, \qquad I_{1} = \frac{I_{2}}{a} = \frac{1.25\ \mathrm{kA}_{RMS}}{8} = 156.25\ \mathrm{A}_{RMS}
\]
\[
P_{line} = I_{line}^{2} R_{line} = (156.25\ \mathrm{A}_{RMS})^{2}(2\ \Omega) = 48.8\ \mathrm{kW}
\]
\[
\eta = \frac{P_{useful}}{P_{wasted} + P_{useful}} \cdot 100
= \frac{P_{MOB}}{P_{line} + P_{MOB}} \cdot 100
= \frac{150}{48.8 + 150} \cdot 100
= 75.4\%
\]
\[
V_{S} = \frac{P_{S}}{I_{1}} = \frac{150\ \mathrm{kW} + 48.8\ \mathrm{kW}}{156.25\ \mathrm{A}_{RMS}}
= 1.27\ \mathrm{kV}_{RMS}
\]
An Air Force Base receives power from a power station located 200 km away. The power station uses a step-up transformer with \(a = 0.0625\) and the base uses a step down transformer with \(a = 500\). The transmission line has a cumulative resistance of 5 \(\Omega\). If the base consumes an average power of 2.5 MW, what is the source voltage and efficiency of this system?

\[
I_{2,\mathrm{xfmr2}} = \frac{P_{AFB}}{V_{2,\mathrm{xfmr2}}}
= \frac{2.5\ \mathrm{MW}}{120\ \mathrm{V}_{RMS}}
= 20.83\ \mathrm{kA}_{RMS}
\]
\[
a_{\mathrm{xfmr2}} = \frac{I_{2,\mathrm{xfmr2}}}{I_{1,\mathrm{xfmr2}}}, \qquad
I_{1,\mathrm{xfmr2}} = \frac{I_{2,\mathrm{xfmr2}}}{a}
= \frac{20.83\ \mathrm{kA}_{RMS}}{500}
= 41.67\ \mathrm{A}_{RMS}
\]
\[
P_{line} = I_{line}^{2} R_{line} = (41.67\ \mathrm{A}_{RMS})^{2}(5\ \Omega) = 8.68\ \mathrm{kW}
\]
\[
a_{\mathrm{xfmr1}} = \frac{I_{2,\mathrm{xfmr1}}}{I_{1,\mathrm{xfmr1}}}, \qquad
I_{1,\mathrm{xfmr1}} = \frac{I_{2,\mathrm{xfmr1}}}{a}
= \frac{41.67\ \mathrm{A}_{RMS}}{0.0625}
= 666.7\ \mathrm{A}_{RMS}
\]
\[
\eta = \frac{P_{useful}}{P_{wasted} + P_{useful}} \cdot 100
= \frac{P_{AFB}}{P_{line} + P_{AFB}} \cdot 100
= \frac{2.5\ \mathrm{MW}}{8.68\ \mathrm{kW} + 2.5\ \mathrm{MW}} \cdot 100
= 99.7\%
\]
\[
V_{S} = \frac{P_{S}}{I_{1,\mathrm{xfmr1}}}
= \frac{2.5\ \mathrm{MW} + 8.68\ \mathrm{kW}}{666.7\ \mathrm{A}_{RMS}}
= 3.76\ \mathrm{kV}_{RMS}
\]



